Tool:    The Rosetta Stone method is a system of graphical techniques for analyzing both continuous-time and discrete-time (or sampled) systems. It relies strictly on continuous-time Fourier transforms and convolution techniques.

 

            In the Rosetta Stone method, we plot waveforms in the time domain alongside waveforms in the frequency domain.

 

            The application of the Rosetta Stone method to discrete-time systems follows from several key observations:

1)     A sampled waveform is equivalent to the continuous waveform multiplied by an impulse train (or comb function), meaning the sampled waveform is equivalent to a train of impulses whose areas equal sample values.

        where

2)     The Fourier transform of an impulse train is an impulse train, meaning we get a train of impulses in the frequency domain (at harmonics of our sampling frequency).

3)     Multiplication in the time domain corresponds to convolution in the frequency domain (and vice versa), meaning we convolve each of the impulses in the frequency domain with the original signal spectrum:

4)     A delta function convolved with a waveform results produces a copy of the waveform with its origin shifted to the location of the delta function, (meaning we get a copies in the frequency domain of the original signal spectrum located at harmonics of our sampling frequency):

 

           

 

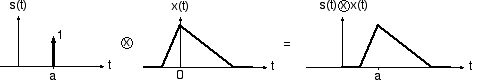
For more information about the Rosetta Stone method, return to the index page and choose a topic.