Ex:          

 

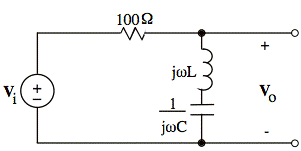
a.   Choose values of L and C that will produce an ωo of 2π⋅104 and a Q of 2.

b.   Calculate β, ωc1, and ωc2.

 

Ans:         a)   L = 3.2 mH, C = 80 nF

b)   β = 31.4 k rad/s, ωC1 = 49.1 k rad/s, ωC2 = 80.5 k rad/s

 

Sol'n:  a)  This is a band reject filter with the following output:

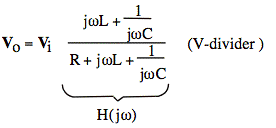
The series L and C will act like a wire at the resonant frequency ωo and an open circuit for ω = 0 (where C acts like an open circuit) and ω → ∞ (where L acts like an open circuit):

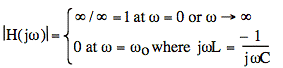
The resonant frequency is found, as always, by solving for the frequency, ωo, where the impedance of the L plus the impedance of the C equals zero:

From the course text, we have an equation for the Q of this particular filter circuit:

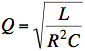
(If necessary, we could also find Q by determining the cutoff frequencies where |H(jω)| = 1/√2. The difference of the cutoff frequencies is the bandwidth, β, and ωo/β = Q.)

Using the equations for ωo and Q, we do some algebra to find C:

Plugging in values given in the problem, we have

Rearranging the equation for Q and using this value of C gives the value for L:

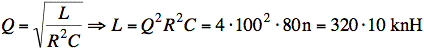
or

Sol'n:  b)  From the course text or calculations of cutoff frequencies as described above, we have equations for cutoff frequencies that apply to simple RLC bandpass and bandreject filters:

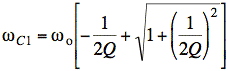
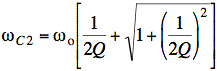
Summing the equations gives a formula for bandwidth, β:

Now we compute ωC1, ωC2:

,           

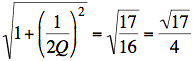
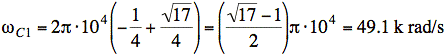
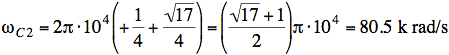
Consistency check: