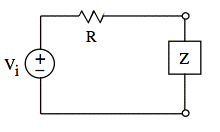
Ex:           a)   Explain what single-resonant circuit to use in the box marked Z to make the voltage across Z a minimum at a specified frequency, ωg.

                  b)   Explain what single-resonant circuit to use in the box marked Z to make the voltage across Z a maximum at a specified frequency, ωg.

Ans:         a)   L in series with C

                  b)   L in parallel with C

 

Sol'n: a)  The voltage across Z is given by the voltage divider formula:

H(jω) 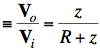       where z is impedance in box

We want |H(jω)| = 0 for specified ωg. So we want z = 0 at ωg.

For L in series with C, we have z = jωL + −j/(ωC). z = 0 at

.

In other words, the series LC looks like a wire at resonant frequency.

We set ωo = ωg, or LC = 1/(ωo)2.

             b)  The voltage across Z is given by the voltage divider formula:

H(jω)        where z is impedance in box

We want |H(jω)| = as large as possible for specified ωg. The solution is to set z = ∞ (or 1/z = 0) at ωg.

For L in parallel with C, we have 1/z = 1/(jωL) + jωC. 1/z = 0 at

.

In other words, the parallel LC looks like an open circuit at resonant frequency.

We set ωo = ωg, or LC = 1/(ωo)2. Note: the same values of L and C will work for both cases. The difference between the two cases is the configuration of the L and C.