Ex:           The circuit shown below is a wave trap, used to prevent the signal from an amateur radio transmitter from entering the input of a TV receiver. Choose proper values of L and C if the transmitter frequency is 50 MHz, and R does not affect the resonant frequency appreciably. Explain how the circuit works. The bottom edge of Channel 2 is at 54 MHz.

What value of R would be required to make |Z| at 54 MHz of one of the resonant circuits equal to 1/10 of its value at resonance and what value of impedance would that be at 54 MHz?

Note: the frequencies here are in units of Hz rather than rad/s.

Ans:         There is no unique answer. For C = 100 pF, then L = 0.101 μH, R ≈ 0.492 Ω, |Z| ≈ 205 Ω at 54 MHz.

 

Sol'n:      The idea is that L parallel C will act like an open circuit at resonance. This prevents the interfering signal from reaching the receiver. With the R included, (but relatively small), the resonant frequency remains approximately the same:

In units of Hz, we have

Any L and C satisfying the following equation will yield the correct resonant frequency:

One solution is C = 100 pF and L = 0.101 μH.

Now we find the value for R.

At resonance, we have equal but opposite reactances for the L and C.

Define the reactances at ωo to be +jX and -jX. From the definition of ωo, we have X = √(L/C) = 31.8 Ω.

At ωo, the impedance, zo, of one side of the trap circuit, (i.e., one C in parallel with an L plus an R), is

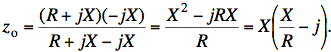
For a frequency, kwo, our L and C reactances become jkX and −jX/k, and we have

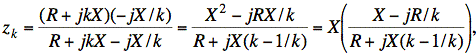
or

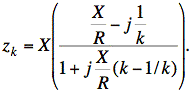
We want |zk/zo| = 1/10 when k = 54 MHz/50MHz = 1.08.

If we define B ≡ X/R, we have

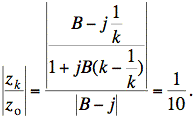
At this point, it is prudent to attempt an approximation. Because k ≈ 1, we may approximate B − j/k as B − j and cancel terms to obtain a simpler equation:

Inverting both sides and applying the definition of magnitude, we have

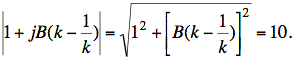
Solving for B, we have

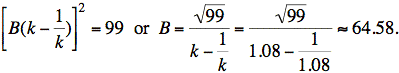
Using R = X/B = 31.8 Ω/64.58, we have R = 0.492 Ω.

At 54 MHz, we have

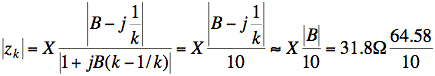
We obtain |zk| ≈ 205 Ω at 54 MHz.