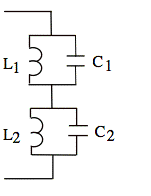
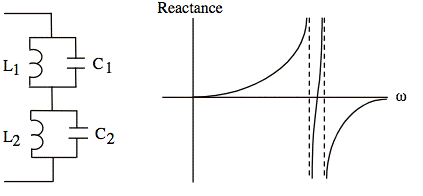
Ex:           In the circuit below, L1C1 = 0.8 L2C2. Draw reactance curves for this configuration to illustrate the location of all of the series and parallel resonant frequencies. Does the total circuit appear to be inductive or capacitive at very low frequencies? Does the total circuit appear to be inductive or capacitive at frequencies well above both of the parallel resonant frequencies?

Ans:         The general shape of the curve is shown below. The highest and lowest resonant frequencies, indicated by dashed lines, are at frequencies whose ratio is 1/√0.8 ≈ 0.9. There is also a resonance where the reactance passes through zero. The frequency of this resonance is

At low frequency, the circuit looks inductive. At high frequency, the circuit looks capacitive.

 

Sol'n:      A parallel L and C looks like an open circuit at resonance. If either of the L parallel C circuits looks like an open circuit, the entire circuit looks like an open circuit. Thus, we have resonant frequencies ω1 and ω2:

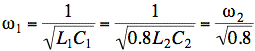
At an intermediate frequency, the L1 and C1 circuit still looks inductive and the L2 and C2 circuit looks capacitive. At some frequency, the impedances exactly cancel. We can calculate that frequency in terms of resonant frequencies. We begin by writing the equation for the total impedance:

Dividing the top and bottom of each term by L gives an expression involving only resonant frequencies:

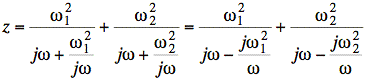
Now we rearrange and solve for z = 0:

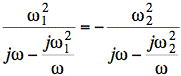
We invert both sides, divide by j, and multiply by ω:

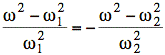
Put both terms containing ω on the left:

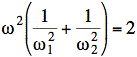
Replacing ω1 with it's value in terms of ω2 yields our final result:

Check:     The frequency must be between ω1 and ω2. Because the factor multiplying ω2 is the square root of one over the average of the squared resonant frequencies, its value is between ω1 and ω2. √

Check:     The frequency must be symmetrical in ω1 and ω2. From the first expression of the last equation above, we see that ω12 is symmetrical in ω1 and ω2. √