Tool:       Cosines and sines of the same or different harmonic frequencies are orthogonal. In other words, the inner product of a cosine and sine over an integer number of cycles is equal to zero:

where is the fundamental frequency and n and m are non-negative integers.

Tool:       Cosines and cosines (or sines and sines) of different harmonic frequencies are orthogonal. In other words, the inner product of cosine and cosine of different frequencies (or sine and sine of different frequencies) over an integer number of cycles is equal to zero:

where is the fundamental frequency and n ≠ m are non-negative integers.

Proof:     We use the following identity:

Using this identity, we have the following calculation of the inner product:

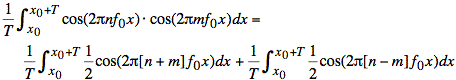
or

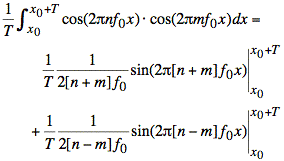
Since n ≠ m, the sines are evaluated at points separated by an integer number of cycles and give the same values. The difference between the value at the upper limit and the value at the lower limit is zero (for both terms). Thus, we have the desired result:

.

Note:       When n = m, the integral expression changes because the second integral becomes the following:

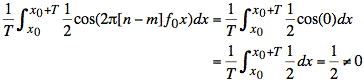
The value is no longer zero.