Ex:           Verify that the power of a square wave calculated directly from

equals the power calculated from Fourier coefficients.

 

Ans:         Power in both cases is p = A2 where A is the amplitude of the square wave.

 

Sol'n:      Consider a square wave, v(t), of period T that is an odd function (positive with value A from t = 0 to t = T/2 and value −A from t = T/2 to t = T).

The square wave, being an odd function, has only sine terms. The square wave, having shift-flip symmetry, has only odd numbered terms.

Direct calculation gives the coefficients for the Fourier series. Because of shift-flip symmetry, we need only integrate from 0 to T/2 and double the value.

v(t) is constant from 0 to T/2.

We may assume any value we desire for T. Here, we will assume T = 2πk. (Note that we may even use a value for T that changes with k.)

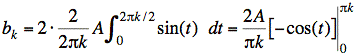
For k odd, −cos(πk) = 1, and we obtain our final answer:

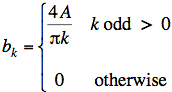
We calculate the average power in terms of Fourier series coefficients by squaring coefficients and multiplying by 1/2 (since this is the average value of a sinusoid squared). Note that we square and multiply by 1 for the DC offset, (i.e., constant offset), a&nu, since this is the average value of 12.

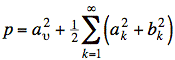
For our Fourier series we have only odd coefficients for sines:

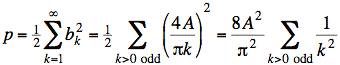
From Tables of Integrals and Other Mathematical Data by Herbert B. Dwight, we have

Thus, we have p = A2.

Calculating the power directly, we compute the energy in one period and divide by the period:

The square wave has values +A and −A and a constant, squared value of A2.

Thus, the power is the same as calculated from the Fourier series.