| Def: |
Fourier Transform of v(t)  |
|
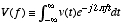 |
| Def: |
Inverse Fourier Transform of v(t)  |
|
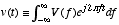 |
| Note: |
The Fourier Transform represents v(t) in terms of a new set of basis functions which are complex frequencies (or sinusoids). |
| Note: |
The Fourier Transform is a correlation calculation that determines how much of each complex frequency (or sinusoid) is in the signal v(t). |
| Note: |
When v(t) is real and even, (i.e., v(t) = v(-t)), the Fourier Transform of v(t) is real and even. This follows from the observation that the imaginary part of the complex frequency is j sin(2pi*ft), an odd function. The integral (from -infinity to infinity) of the product of an even and odd function is equal to zero. Also, the forward and inverse transforms are the same; if we exchange f and t in the transform pair v(t) and V(f) we get the valid transform pair V(t) and v(f). |
| Note: |
When v(t) is real and odd, (i.e., v(t) = -v(-t)), the Fourier Transform of v(t) is imaginary and odd. Also, the forward and inverse transforms are conjugates; if we exchange f and t and change the sign of the transform pair v(t) and V(f) we get the valid transform pair -V(t) and v(f). |