Ex:           Find the inverse Laplace transform of

Sol'n:      We first factor the denominator:

We have complex roots, implying a decaying oscillatory solution with

We may use standard partial fraction techniques, multiplying by one root and evaluating at a value of s that makes that root equal to zero. Writing F(s) directly as a decaying cosine plus a decaying sine is a more direct approach, however:

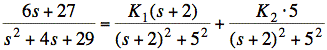
Since the denominators are the same on both sides, we equate the sum of the numerators on the right with the numerator on the left. We start by matching the highest power of s. This requires a value of

Using this value of K1 we choose K2 to satisfy an equation for the constant term:

Our solution is