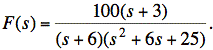Ex:           Plot the poles and zeroes of

 

Ans:        

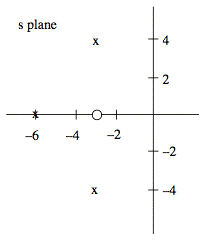
Sol'n:      The zeros, indicated by o's on the pole-zero diagram are the roots of the numerator, (i.e., the values of s that make the numerator equal zero).

The poles, indicated by x's on the pole-zero diagram are the roots of the denominator, (i.e., the values of s that make the denominator equal zero).

 

Since the numerator has only one root, there is only one zero. It is located at s = −3 where s + 3 = 0.

In general the numerator may have any number of roots. In circuit problems, the numerator is typically of lower order than the denominator. Exceptions to this rule occur when differentiation leads to extra factors of s in the numerator.

Since the denominator is of order three, there are three zeros. The denominator is already partially factored. When completely factored it has three terms:

We use the quadratic equation to find the roots, s1 and s2, of the quadratic term and write it as (s − s1)(s − s2). The poles are located at the values of s that make the terms equal zero. Thus, the poles are located at s = −6, s = −3 + j4, and s = −3 − j4.

When the denominator is of higher order than the numerator, (more poles than zeros), we may use partial fractions to find the inverse transform of F(s). If not, we divide the denominator into the numerator (using polynomial division) and take the inverse transforms of the dividend terms (of form ksn where n ≥ 0) and the remainder (which will be in proper form allowing the use of partial fractions).

Note:       When finding poles and zeros, factor out and discard the constant multiplier that equals the coefficient of the highest order term in the numerator divided by the coefficient of the lowest order term of the denominator. In this example, that would be 100/1 equals 100. This is the gain term, and it does not affect the pole-zero diagram. It may be noted somewhere on the diagram, if desired, however.