Nonlinear Systems/Differential Equations

Autonomous differential equations

Form

 

 

Tool:      Autonomous differential equations have the following form:

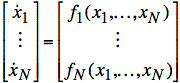                      or    

                  The autonomous form describes nonlinear (or linear) differential equations according to the following rules:

i)    There is a set (or vector, ) of state-space variables with one equation, , for each such variable.

ii)   On the left side of each equation is the first (not second or higher-order) derivative with respect to time of one state variable.

iii)  On the right side of each equation is a function of only state-variables and constants, (no derivatives).

iv)  If time, t, is used as a variable, then it is considered a state variable. It is defined by an equation obeying the above rules. The state variable, x, in the following equation is equal to t:

Note:      By making time a state variable, we may include forcing functions on the right side of equations.

Note:      If the values of the state variables are known, the state of the system is completely known.

Tool:      The functions on the right side must be differentiable at any point where we wish to linearize them.

Tool:      A solution to the autonomous system of equations exists even if the functions on the right side are discontinuous.