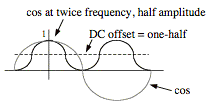Tutorial:   AC POWER

In a linear circuit with sinusoidal source of frequency ω, currents and voltages are sinusoids of frequency ω. Power is still calculated as p = iv. Thus, we multiply sinusoids, although there is typically a phase difference between the current and voltage. We define the phase difference as (θ_v − θ_i). If we also define i_m and v_m as the amplitudes of current and voltage and adjust the origin of time so that θ_i = 0, we have

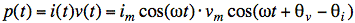
Note that we might try to leave the θ_i in the current term but the result is quite awkward to work with.

We apply a standard trigonometric identity to translate the product of sinusoids into a sum of sinusoids:

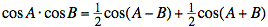
where A − B = θ_v − θ_i and A + B = 2ωt + θ_v − θ_i.

The result is that the power has a constant (or DC) term (that is no longer dependent on time or frequency) and a sinusoidal signal (that has double the frequency of the current and voltage):

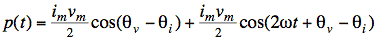
Note also that there is a factor of one-half in both terms. A trick for remembering these features of the power waveform is to consider the power waveform when current and voltage are in phase. In that case, the product of i and v has the shape of cos²(ωt). Sketching cos²(ωt) reveals that it is the sum of cos(2ωt) with amplitude one-half and a DC offset of one-half.

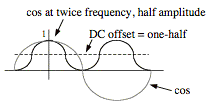
If we now think in terms of frequency 2ω instead of ω we see that the second term of the power expression is a cosinusoid with a magnitude and phase offset. In other words, it is a sinusoidal signal represented in polar form. We may translate it into rectangular form consisting of a pure cosine and a pure sine:

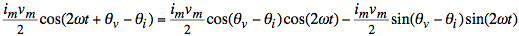
Note that this is only the sinusoidal (or AC) part of the power expression.

To simplify the notation, we define P and Q:

By coincidence, P appears twice in the complete power expression, meaning we need only P and Q rather than three different terms:

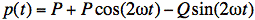
Because we have both P and Q in the AC part of the power, (i.e., the last two terms),we achieve an economy of notation (and possibly a loss of clarity) by ignoring the DC part of the power and then using a phasor representation of the AC part:

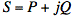
Note that the sign is + for Q in the phasor, whereas the sign is − for Q in the expression for p. Also, this "complex power", S, happens to have, as its real part, the average or DC power P. Strictly speaking, however, the P represents the cosine part of the AC power.

If we use phasors for the original current and voltage waveforms, we may derive the following identities:

Once we have found S, we know P and Q and, hence, we know the complete power waveform, p(t).