By: Neil E. Cotter	Probability
		Basic probability
		Law of Total Probability
		ex 1

---

Ex: A company has found that a certain fraction of the parts it orders are counterfeit. That fraction depends on which company the parts were ordered from. The parts are mixed together in a stockroom, so the selection of parts may be viewed as an experiment in probability. The following information is known.

A ≡ event that parts selected are from company A

B ≡ event that parts selected are from company B

C ≡ event that parts selected are counterfeit

P(A) = 0.35

P(B) = 0.25

P(C) = 0.10

P(A∩C) = 0.08

P(B∩C) = 0.01

What is the probability of picking a part that is counterfeit and not from either company A or B? Note that we may write this probability as P(C∩(A∩B)')

Sol'n: Since we are calculating the probability of an intersection, we consider using the law of total probability. To do so, we need a partition of the sample space, S, of all possible outcomes. We may safely assume that A and B are mutually exclusive, since they are distinct companies. To complete the partition, we use the rest of S. That is, we use (A∩B)'. Our partition is A, B, and (A∩B)'.

Venn diagram:

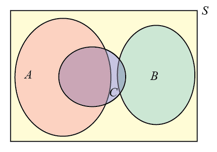
We want the area in C and between A and B in the Venn diagram. By the law of total probability, we use the following calculation of the probability of C:

P(C) = P(A∩C) + P(B∩C) + P(C∩(A∩B)')

We know the values of all the terms except the one we are looking for.

0.10 = 0.08 + 0.01 + P(C∩(A∩B)')

We solve for our unknown value to complete the solution.

P(C∩(A∩B)') = 0.10 – (0.08 + 0.01) = 0.01