|
|
By: Neil E. Cotter |
Probability |
|
|
|
Basic probability |
|
|
|
Venn diagrams |
|
|
|
Example 1 |
|
|
|
|
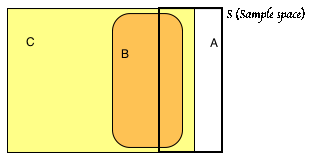
Ex: Draw all possible representative Venn diagrams consistent with the following information about events A, B, and C: (use areas approximating probabilities)
P(A) = 0.225 P(B) = 0.4 P(C) = 0.9
P(A Ç B¢) = 0.125 P(B Ç C) = 0.4
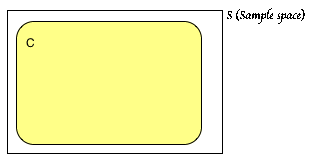
Sol'n: We start our Venn diagram by drawing the most probable event, C:
Total area of the diagram = total probability of sample space = 1. The area for event C = P(C) = 0.9.
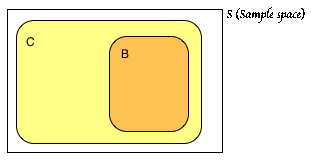
We observe that P(B) = P(B Ç C) = 0.4. This implies that event B lies entirely inside event C. (Note: strictly speaking, event B might contain outcomes of zero probability that lie outside C. Thus, we are ignoring such outcomes. This is not a serious problem since the probability of these outcomes is zero.)
Given P(A) = 0.225 and P(A Ç B¢) = 0.125, we apply the law of total probability that says P(A Ç B) + P(A Ç B¢) = P(A) to conclude that P(A Ç B) = 0.1.
What we still lack is information about the intersection of A and C. It is possible that A lies entirely in C. So one possible representative diagram is as follows:
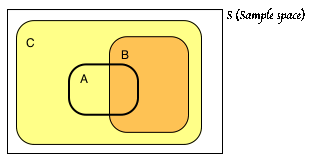
We know that A intersects B, but might the rest of A lie outside C? Or does A have to intersect the part of C outside of B? The probability of being in the part of A lying outside of B is P(A Ç B¢) = 0.125. But P(C¢) = 1 – P(C) = 0.1. Thus, there is too little room outside of C to fit all of A not lying in B. The minimum value for P(A Ç B¢) is 0.025 as shown in the other representative diagram: