Conceptual Tools

	By: Neil E. Cotter	Probability
		Basic probability
		Venn diagrams
		Example 2

Ex: An engineering firm working in Iraq is concerned about attacks on electrical power generating plants. In the article "Re-engineering Iraq," by Glenn Zorpette in IEEE Spectrum, Vol. 43, no. 2 (NA), February 2006, p. 22, electrical power generating plants are categorized as belonging to one of three groups:

C = combustion plants

H = hydroelectric plants

T = thermal plants

For the sake of this problem, we assume every plant in Iraq belongs to one and only one of these three groups, C, H, or T.

We will also consider which of the various power plants are in the "Big" category:

B = Big plants (that generate more than 200 MW)

Based on the assumption that all plants are equally likely to be attacked, the data in the Spectrum article gives the following probabilities for the type of plant that will be attacked next:

P(C) = 16/36 P(H) = 9/36 P(T) = 11/36

P(B) = 18/36 P(HB) =4/36 P(TB) = 7/36

a) Find P(T¢). That is, find the probability that the next plant attacked is not in category T.

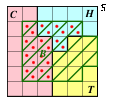
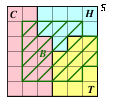
b) Draw a Venn diagram showing events C, H, and T. (You do not have to show B.) On the diagram, use area to represent the probability of each event, C, H, and T, and show intersections accurately. Note that each small box in the Venn diagram has area 1/36.

c) Find the the value of P((CH)B). Show your reasoning.

Sol'n: a) P(T¢) = 1 – P(T) = 1 – 11/36 = 25/36.

Note: T and the complement of T form a total partition of the sample space, S. That is, they are mutually exclusive, (i.e., do not overlap), and they are exhaustive, (i.e., their union contains every possible outcome). It follows that P(T) + P(T¢) = P(S) = 1.

b) Since "we assume every plant in Iraq belongs to one and only one of these three groups, C, H, or T", the three groups form a total partition of the sample space, S. They do not intersect, and they completely cover S. The size of each area is equal to the probability of the corresponding event. One way of drawing the diagram is shown below.

c) Since C, H, and T form a total partition of the sample space, we can apply the Law of Total Probability to write an expression for P(B):

P(B) = P(CB) + P(HB) + P(TB)

Solving for the only unknown value, which is P(CB), gives the following result:

P(CB) = P(B) – (P(HB) + P(TB)) = 18/36 – (4/36 + 7/36)

P(CB) = 7/36

The Venn diagram below illustrates the above calculations.

From the diagram, we see that (CH)B = (CB)(HB). Thus, we can assert that P((CH)B) = P((CB)(HB)). Furthermore, the two sets in the union are mutually exclusive since C and H are mutually exclusive. It follows that we can sum the probabilities: