Ex:            Three companies, A, B, and C provide cell-phone coverage in a city. For a randomly chosen location in the city, the probability of coverage for the first two companies is as follows:

          P(A) = 0.8                     P(B) = 0.75

The following probabilities of coverage by company A or B or by B and C are also known:

                      

a)     Find the probability, P(A'), of not having coverage from company A.

b)     Find the probability, , of having coverage from both company A and company B.

c)     Company A claims their probability of coverage, P(A), is higher than company C's probability of coverage, P(C). Determine whether this statement is true or false, and justify your answer.

d)     Find the smallest possible value the probability, , of having coverage from company B or company C or both can be. (In case you have two cell phones...)

Sol'n:       The Venn diagram below shows the information that is known about events A, B, and C. Areas in the diagram correspond to probabilities.

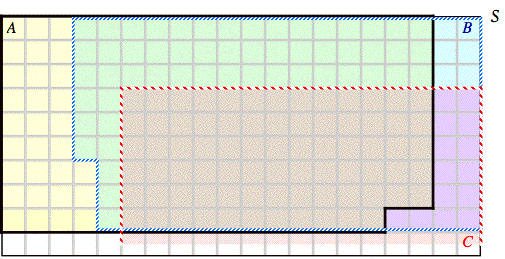
Because P(C) is unknown, the area for C is shown open-ended.

We must be careful to draw only conclusions that follow from the information given in the problem. The exact value of , for example, is unknown, although the diagram shows it as 0.38.

             a)  For any event A, the probability of the complement of A, A', is one minus the probability of A:

P(A') = 1 − P(A)

Using numerical values yields the answer:

P(A') = 1 − P(A) = 1 − 0.8

Note:       A and A' form a (total) partition. Together they account for all possibilities, (i.e., the entire sample space), and they are mutually exclusive.

             b) To find , we use the equation for :

Rearranging the equation yields the value of :

Substituting numerical values given in the problem, we have the following result:

We could also use the Venn diagram and determine the area of the intersection of A and B. Counting the green and brown squares in the intersection gives a value of 130 squares/200 squares in the intersection of A and B. In other words, .

             c)  The largest value that P(C) may possibly have, given the information in the problem, occurs if C includes all the area outside of B. In other words, the largest possible value for P(C) is :

Using the Venn Diagram, we would have the following picture:

Everything inside the dashed red line represents that maximum possible size of C. We count 140 squares lying in C out of the total of 200. In other words, the maximum possible value of C is 140/200 = 0.7.

             d) Without further knowledge, the smallest possible value of is the larger of P(B) and P(C). This follows because the union of two events includes both events. Thus, and . Since P(C) is unspecified, it is possible that C lies entirely in B. This yields the smallest possible value for P(C) and, therefore, for . In that case, , since having C inside B implies P(C) > P(B):