Ex:            Consider the problem of speech recognition. A parent speaking to a baby says a word that sounds like "yoyo" to the baby. The baby tries to decide whether the word was "yes" or "no". In other words, the baby tries to determine which of the following probabilities is larger:

P("yes" was said | "yoyo" was heard) ≡ P(yes | yoyo)

P("no" was said | "yoyo" was heard) ≡ P(no | yoyo)

The baby knows the following probabilities that represent how often the parent says "yes" or "no" in general:

P(yes) = 5/6 (the parent is permissive most of the time)

P(no) = 1/6

The baby has learned the following probabilities from experience:

P("yoyo" was heard | "yes" was said) = 1/2⋅P("yoyo" was heard | "no" was said)

or

P(yoyo | yes) = 1/2⋅P(yoyo | no)

Note:       P(yoyo | yes) and P(yoyo | no) need not sum to unity. Nevertheless, we can solve the problem using only the ratio of these probabilities.

Sol'n:       Using Bayes' Theorem, we calculate the desired probability:

Note:       We lack the information to calculate the denominator, (even in expanded Bayes' form), in the above equations. We can solve the problem without this information, however.

We take the ratio of the equations to solve the problem and eliminate the unknown quantity, P(yoyo).

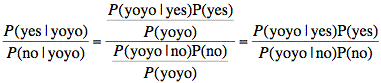
or

Thus, it is more likely that the parent said "yes" even though the probability that the baby will hear "yoyo" when the parent says "no" is higher than the probability that the baby will hear "yoyo" when the parent says "yes".