Ex:           A particular cell-phone base station provides service to 10,000 cell phones. The base station can handle 250 simultaneous calls. If the number of calls exceeds 250, the excess calls will be blocked. At any given time, the probability that a randomly chosen cell phone is making a phone call is p = 0.02.

a)      Find the mean number of calls at a given time.

b)      Find the variance of the number of calls at a given time.

c)      Write a formula for the probability that the number of calls at a given time will exceed 250. Write only the formula, the calculation is intractable.

d)      Use the gaussian approximation to the binomial distribution to estimate the probability that the number of calls will exceed 250 at a given time.

Sol'n: a)  For Bernoulli trials, the mean number of successes in n trials is μ = np where p is the probability of success for one trial. Using numbers from this problem, n = 10,000 cell phones, and the probability of a cell phone being in use is p = 0.02. The mean number of calls at a given time is μ = np = 10,000⋅0.02 = 200.

             b) For Bernoulli trials, the variance of the number of successes in n trials is σ2 = npq where q is the probability of failure for one trial: q = 1 − p. Using numbers from this problem the probability of a cell phone not being in use is q = 1 − 0.02 = 0.98. The variance of the number of calls at a given time is σ2 = npq = 10,000⋅0.02⋅0.98 = 196.

             c)  For Bernoulli trials, the probability of m successes in n trials is given by the binomial distribution:

To find P(m > 250, n = 10,000), (i.e., the probability of m > 250 calls in progress for n = 10,000 cell phones), we sum terms from the binomial distribution:

P(m > 250, n = 10,000) =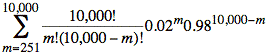

An alternative, simpler formula is found by computing one minus the probability that the number of calls is at most 250.

P(m > 250, n = 10,000) = 1 − P(m ≤ 250, n = 10,000)

or

P(m > 250, n = 10,000) =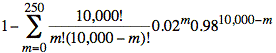

Note that we include the possibility that m = 0 in this calculation since it is possible that no cell phones are in use.

             d) The gaussian approximation to the binomial applies when p is close to 1/2 or n is very large and p is not too close to 0 or 1. The idea is to approximate a sum such as that in part (c) by using the area under a gaussian probability density function with the same mean and variance as the binomial distribution. Thus, we use a gaussian distribution with the following mean and variance:

μ = 200        σ2 = 196 (or σ = 14)

In order to use tables for the value of the cumulative distribution function, F(x), for a gaussian distribution, we convert values into their equivalent value, z, for a standard gaussian distribution, (i.e., one with mean = 0 and variance = 1):

Here, we are interested in x = 250 phone calls, and we want to compute the area under the gaussian to the right of x. Since x only has integer values, however, we actually get a slightly better estimate if we use x = 250.5.

Using a table of cumulative distribution, F(z) = P(Z < z), for a standard gaussian, we get the following value:

F(3.607) = 0.999845

We use 1 − F(z) since we want the area under the gaussian to the right of z. This gives our final answer for the approximate probability that more than 250 cell phones are in use.

P(m > 250 cell phones in use) ≈ 0.000155 = 1.55⋅10−4

There is less than one chance in 5000 that the cell phone network will be overloaded.

Note:      We have assumed the gaussian approximation is valid even though p is close to zero. We do have a large number of samples, but the result should be used with caution.

Note:      A more realistic treatment of this problem would consider the rate at which we sample cell phone usage. As now stated, the problem allows sampling at infinitely closely spaced points, meaning the network might fail many times a second. To cure this shortcoming, we could assume the process is sampled only as often as the average length of a cell-phone call.