Ex:           A raffle is being held. 26 people, including Ann, Ben, and Cam, each have one raffle ticket. Three tickets are drawn for three identical prizes. The tickets are set aside after they are drawn out of a hat, meaning each person can win at most one prize.

Assuming all tickets are equally likely to be picked, find the probability that Ann, Ben, and Cam win the three prizes.

Sol'n:      Since the three prizes are the same, the order in which tickets are selected is unimportant in this problem. Thus, we may use combinatorics to find the solution. Interestingly, we may also use permutations. Since the tickets are picked in some order, the permutations approach seems natural, and we make it our starting point.

The probability of the event that Ann, Ben, and Cam win the three prizes is equal to the number of outcomes with Ann, Ben, and Cam as winners divided by the total number of possible outcomes.

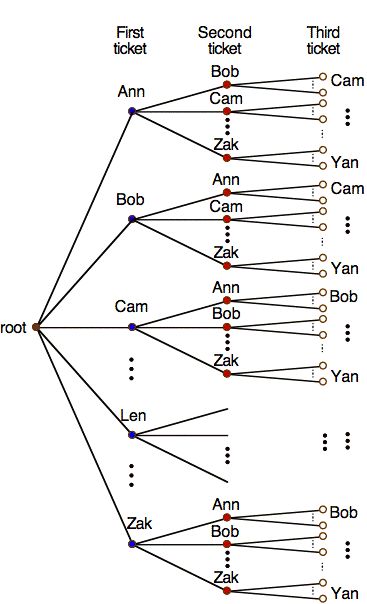
We first consider how to calculate the total number of outcomes. Although only three tickets will be drawn from the hat, we consider drawing all the tickets one-by-one out of the hat. When picking the first ticket, the number of tickets to choose from is 26. When picking the second ticket, the number of tickets to choose from is 25, and etc. If we keep track of the order of the tickets drawn, we have 26⋅25⋅24⋅...⋅1 = 26! possible outcomes.

If we consider only the first three tickets drawn, we stop the process after the first three steps, and the number of possible outcomes is 26⋅25⋅24 = 25!/23! Another way of viewing this result is to observe that there are 23! ways of picking the tickets after the first three. These are counted as different outcomes if we draw all of the tickets out of the hat, yet those outcomes all have the same first three tickets. This means that we overcount the number of outcomes that give the same first three tickets by a factor of 23! Thus, we should divide 26! by 23! to get the number of ways of picking the first three tickets.

To recap, the number of ways of picking the first three tickets when order is taken into account is 26⋅25⋅24 = 26!/23! This is the permutation coefficient, 26P3 for 26 items chosen 3 at a time. Note that the word "permutation" reflects the idea that we do care about the order in which tickets are selected. If the order is permuted, we have a different oucome.

26P3 =

The tree structure shown below illustrates the calculation:

In general we have

nPm = .

If the order of picking tickets is unimportant, as is true in this problem, then we have a smaller number of outcomes. The number of ways of picking the same set of three tickets is 3⋅2⋅1 = 3! = 3P3. This is the number of ways of choosing three items, taken three at a time, when order is taken into account. We have overcounted by this factor. Thus, the total number of ways of picking the first three items when order is unimportant is 26P3/3P3. This is the combinatorial coefficient:

26C3 =

In general w have

nCm = .

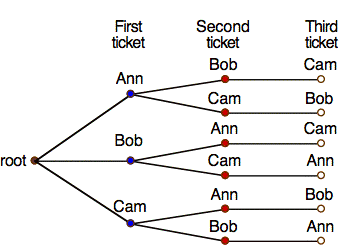
Now we consider the number of outcomes with Ann, Ben, and Cam as winners. If we take the order of selecting tickets into account, then the number of ways of picking tickets for Ann, Ben, and Cam is 3⋅2⋅1 = 3! = 3P3. See the diagram illustrating the calculation, below.

If order is unimportant, which is true here, then we must divide this number by the number of ways of rearranging the three tickets for Ann, Ben, and Cam. Thus, we have 3P3/3P3 = 3C3 = 1 outcome consisting of Ann, Ben, and Cam. Upon reflection, the number of sets consisting of Ann, Ben, and Cam is just one, namely the set consisting of Ann, Ben, and Cam.

Finally, we compute the probability of picking the tickets for Ann, Ben, and Cam as the ratio of the number of outcomes consisting of tickets for Ann, Ben, and Cam to the total number of possible outcomes.

P(Ann, Ben, and Cam win) =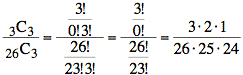

or

P(Ann, Ben, and Cam win) =

As is often the case, we can get the same answer by only considering outcomes in which order is taken into account. We will overcount the outcomes for Ann, Ben, and Cam winning, but we will overcount all the outcomes by the same factor:

P(Ann, Ben, and Cam win) =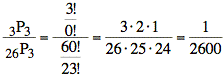

Note:      This dichotomy of approaches can be very confusing. Since either approach is valid, it is advisable to focus on one view or the other and become comfortable with one's own style of solving combinatorics problems.