Ex:           A wealthy engineer working in a luxury villa in the Caribbean is using a satellite link for her internet connection. To improve reliability, the network is redundant, having two possible paths to the Internet Service Provider (ISP). One path uses two satellites in sequence, whereas the other path uses a single satellite.

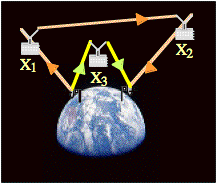
At the time of this writing, the sun is dropping below the horizon, as are the satellites. There is a beautiful sunset, but the communications are intermittent.

The probability of a packet passing successfully through satellite X1 is denoted as P(X1 = 1) with value P(X1 = 1) = 0.8. The probability of a packet not passing successfully through satellite X1 is denoted as P(X1 = 0) with value P(X1 = 0) = 1 − P(X1 = 1) = 0.2. Using similar notation, P(X2 = 1) = 0.75 and P(X3 = 1) = 0.6. Events X1, X2, and X3 are independent.

Using this information, determine the probability that a packet will get through one or both of the two pathways.

Sol'n:      One way to solve this problem is to enumerate every possible outcome where outcomes are written as triplets (X1, X2, X3). Since X1, X2, and X3 are independent, the probability of any triplet is equal to the product of the probabilities of the individual paths, X1, X2, and X3.

Outcome	Packet transmission	Probability
(X1, X2, X3)	(1 = success)	P(X1, X2, X3) = P(X1)⋅P(X2)⋅P(X3)
0 0 0	0	0.2 ⋅ 0.25 ⋅ 0.4 = 0.02
0 0 1	1	0.2 ⋅ 0.25 ⋅ 0.6 = 0.03
0 1 0	0	0.2 ⋅ 0.75 ⋅ 0.4 = 0.06
0 1 1	1	0.2 ⋅ 0.75 ⋅ 0.6 = 0.09
1 0 0	0	0.8 ⋅ 0.25 ⋅ 0.4 = 0.08
1 0 1	1	0.8 ⋅ 0.25 ⋅ 0.6 = 0.12
1 1 0	1	0.8 ⋅ 0.75 ⋅ 0.4 = 0.24
1 1 1	1	0.8 ⋅ 0.75 ⋅ 0.6 = 0.36

Note:      The sum of all probabilities in the right column must sum to one.

The sum of outcomes that result in successful packet transmission is

P(success)   = P(0 0 1) + P(0 1 1) + P(1 0 1) + P(1 1 0) + P(1 1 1)

                    = 0.03 + 0.09 + 0.12 + 0.24 + 0.36 = 0.84.

This works in this example, but enumerating all examples is impractical in many cases. An alternative approach involves calculating the probabilities of success for each path. Using set theory, we have

or

Note:      An event such as X1 = 1 specifies only the value of X1, meaning that this event includes all the possible values of X2 and X3. That is, the event X1 = 1 is the following set of outcomes

X1 = 1 ≡ {(X1, X2, X3) = (1, 0, 0), (1,0,1), (1, 1, 0), or (1, 1, 1)}.

If outcomes are written in terms of coordinates or axes, all unspecified axes can have any value. Writing all the possible values is usually impractical but understanding the concept is helpful when thinking about events as sets.

When the axes are independent, we may ignore all the possible values for the unspecified axes and use, e.g., P(X1 = 1).

Using probabilities of sets, we have

                        .

Thinking of all the outcomes in each event, we would compute our answer as follows:

                                    = 0.24 + 0.36 = 0.60

                   

                 = 0.03 + 0.09 + 0.12 + 0.36 = 0.60

= 0.36

= 0.60 + 0.60 − 0.36 = 0.84

If exploit the independence of X1, X2, and X3, we compute our answer as follows:

= 0.8 ⋅ 0.75 = 0.6

= 0.60

= 0.36

= 0.60 + 0.60 − 0.36 = 0.84

A third, much simpler approach, is to calculate the probability of not successfully transmitting a packet and then computing one minus that probability.

= 1 − P(failure)

This is simpler because the only way to have a failure of transmission is to have failure for both possible paths. Exploiting independence, we have

.

Employing the same type of logic, we can calculate the first term on the right by considering the complement and subtracting its probability from 1.

P(X1 = 0 or X2 = 0) = 1 − P(X1 = 1 and X2 = 1)

                                 = 1 − P(X1 = 1) ⋅ P(X2 = 1)

                                 = 1 − 0.8 ⋅ 0.75 = 1 − 0.6 = 0.4

Thus we have

= 1 − 0.4 ⋅ 0.4 = 1 − 0.16 = 0.84.