Ex:           Five fair 6-sided dice are rolled. Find the probability that exactly three dice show the same number, (i.e., three of a kind), and the remaining two dice show the same number, (i.e., a pair). This is known as a "full house". Note that the number showing on the pair must be different from the number showing on the three of a kind, as otherwise we would have five-of-a-kind.

Sol'n:      P(full house) =

The primary difficulty here is deciding how to define an outcome so we can avoid distorting probabilities.

One incorrect approach, for example, is to equate outcomes with categories such as one pair, two pairs, three-of-a-kind, full house, four-of-a-kind, etc. This distorts probabilities because it is clearly much more likely that we will have a pair than that we will have four-of-a-kind.

Another incorrect approach, for example, is to equate outcomes with the unique sets of numbers on the dice when the numbers are listed from smallest to largest. This distorts probabilities because a set of numbers such as five 1's requires every die to show a 1, whereas a set of numbers such as 1, 2, 3, 4, 5 allows us to exchange numbers on any two dice and still have the same outcome.

One correct approach begins by identifying each die with a unique label. Since the dice are physically distinct objects, this has no effect on the probabilities. For simplicity, we may even assume that the labels are colors and we may imagine that the dice actually have those colors. We may also assume that the dice are rolled in a specific color order. Since the number rolled on each die is independent of numbers on other dice, rolling the dice in color-order gives the same probabilities of outcomes as rolling them all at once.

We calculate the total number of all possible outcomes by counting all the combinations of numbers that can appear on the five dice. We may imagine making a diagram of all the possible outcomes, as shown below. The numbers are the same as counting in base 6.

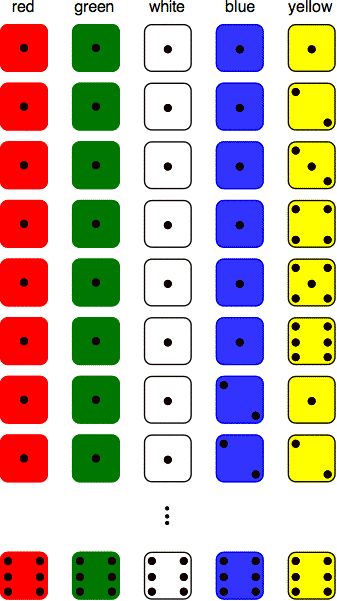
The last die may have six values. For each of these six values, the second-to-last die may have six values. Thus, we have 6⋅6 = 36 possible outcomes for the last two dice. By extension, we have a total of 65 = 7776 possible outcomes for all five dice.

Turning to the number of full-house outcomes, the illustration below shows an example of a full house achieved by rolling the dice in order. Note that the three-of-a-kind may occur on non-adjacent dice.

Another roll that is counted as a separate outcome in the correct approach but would have been counted as the same outcome in the two incorrect approaches discussed earlier is shown below.

To correctly count the number of full houses, we first consider what the numbers are in the 3-of-a-kind and in the pair. Referring to the possibilities as "varieties" of full houses, the number of varieties is the product of the number of numbers for the 3-of-a-kind and the number of numbers for the pair.

# varieties = # 3-of-a-kind numbers ⋅ # pair numbers

We have six choices for the number for the 3-of-a-kind. Once we choose this number, we must choose a different number for the pair. Otherwise, we will have 5-of-a-kind. Thus, we have 6⋅5 = 30 varieties of full houses.

# varieties = 30

Note that we would get the same result if we chose the number for the pair first, (6 choices), and the 3-of-a-kind second, (5 choices).

Before proceeding, we consider whether all the full houses are distinct. In other words, we consider whether the way we assign the numbers in a full house to the different dice can result in one full house giving the same outcome as another. In the present case, if a roll is a full house, there will be a unique number showing for the 3-of-a-kind and a unique number showing for the pair. This will correspond to exactly one of the 30 possible ways to choose the numbers for the 3-of-a-kind and pair. Since the full house accounts for all five dice, any uncertainty that might result from numbers on extra dice, (which would apply if we were considering only the probability of getting a certain 3-of-a-kind, for example), is eliminated. Thus, permuting the assignment of numbers to dice cannot cause one variety of full house to look like another. The varieties of full houses form a partition of all possible full houses.

By symmetry, each of the 30 different full houses has the same probability. Thus, we need only determine how many ways there are to assign numbers to dice for one particular full house, say three 1's and two 2's.

Starting with the three 1's, we are interested only in which three dice are assigned 1's. Although we might assign them in a particular order, only the set of dice assigned 1's matters. Conversely, we could assume we work from left to right when assigning the dice that are 1's. All that matters is the set of dice we pick. Thus, we use a combinatoric coefficient.

# ways to assign three 1's = 5C3 =

Once we choose the set of dice for the 1's, the set of dice for the 2's has to be the remaining dice. In other words, there is only one way to pick the dice the 2's are assigned to.

Combining results—by multiplying—we have the total number of full houses.

# full houses = # varieties of full houses

                      ⋅ # ways to assign three 1's ⋅ # ways to assign two 2's
                         = 30 ⋅ 10 ⋅ 1
                         = 300

The probability of a full house is the number of possible full houses divided by the total number of possible outcomes with five dice.

P(full house) =

In other words, about one out of 26 rolls will be a full house.