Ex:           Four computers, R, G, B, and P, each have 13 network ports and form a cluster running programs written for multiple processors running in parallel. Owing to a bug in the code, the entire system will crash if two programs use port number 1, even when they are on different computers. The port allocation routine picks ports at random from all those not currently in use. One program is using ports B1 and P9, as shown in yellow below. Another program is using port G13, as shown in light orange.

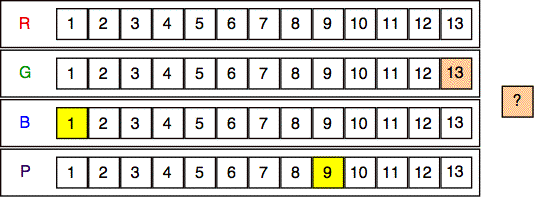
Find the probability that the next port chosen is a port 1. That is, find the probability of R1, G1, or P1.

Sol'n:      The total number of ports is 52. Three, B1, P9, and G13, are in use. Thus, there are 49 ports available. The probability of picking one of the three port 1's is 3/49.

P(B1, P9, G13) =

 

Note:      If none of the port 1's were already in use, the probability of picking a port 1 given three other ports in use would be 4/49. Thus, the ratio of probabilities with and without a port 1 already in use is 4 to 3.