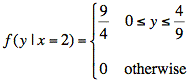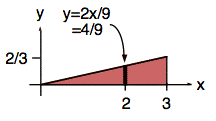Ex:           Given joint probability density function f(x, y) = 1 on the area of the x,y-plane shown below, find the conditional probability density function .

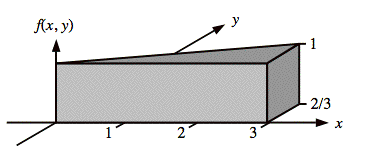
Sol'n:      The illustration below shows a 3-dimensional view of f(x, y).

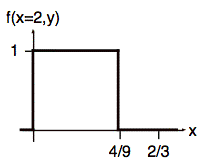
The conditional probability, f(y | x = 2), is equal to the cross-section of f(x, y) in the y direction at x = 2 scaled vertically to make the area equal to one. The illustration below shows the cross-section at x = 2.

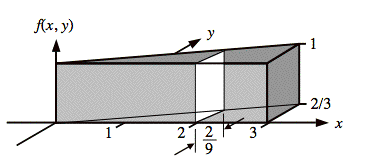
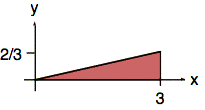
The width of the cross-section is apparent in the following top view of the support (or footprint) of f(x, y) in the xy-plane.

This cross-section is a function of y as shown below.

We scale the figure vertically to obtain area equal to one. That is, we multiply by 9/4:

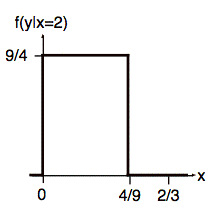
If we take a purely mathematical approach to finding f(y | x = 2), we use the definition of conditional probability:

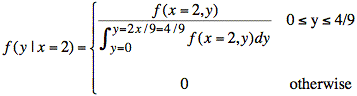
Substituting f(x = 2, y) = 1, we complete the calculation:

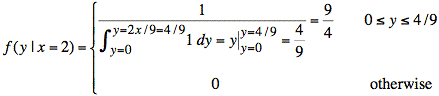
The equation for f(y | x = 2) also captures the information in the above plot: