Ex:           A joint probability density function is defined as follows:

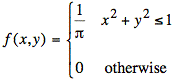
Find the conditional probability .

Sol'n:      The region, x2 + y2 ≤ 1, on which f(x, y) ≠ 0 is called the support of f(x, y). It is a circle of radius one, centered on the origin, as shown below. The diagram also shows the horizontal segment that is the support for the cross-section that forms the basis for .

The diagram shows that the cross-section extends from to . The conditional probability, , is a scaled version of the cross section of f(x, y) at y = 1/2. The illustration, below, shows the 3-dimensional shape of f(x, y) and the cross section in the x direction at y = 1/2.

The probability density function that is is the above cross-section scaled vertically to have an area equal to one. Since the cross-section is rectangular, this means the height will be scaled up to a value of 1/width where the width is :

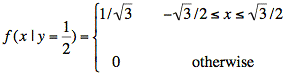
Taking a more strictly mathematical approach, we would integrate to find the area of the cross section and divide the cross-section by the result:

or

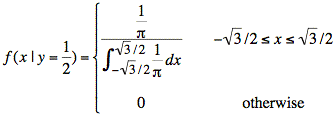
The integral is the difference of the limits multiplied by 1/π.

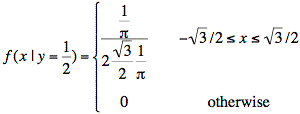
Canceling out terms yields the same result as before: