Ex:           A joint probability density function is defined as follows:

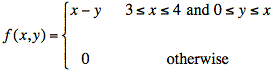
Find the conditional probability f(y | x = 3).

Sol'n:      The region, 3 ≤ y ≤ 4 and 0 ≤ y ≤ x, on which f(x, y) ≠ 0 is the support of f(x, y). It is a trapezoid, as shown below. The diagram also shows the vertical segment for x = 3.

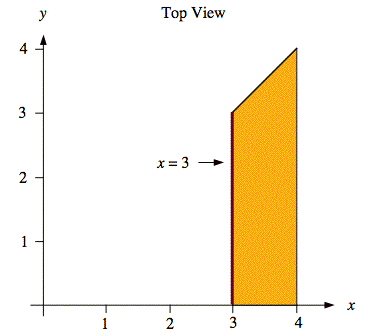
The illustration, below, shows the 3-dimensional shape of f(x, y). The figure also shows cross-sections at x = 3. The density function for f(y | x = 3) is equal to the area of the cross-section of f(x, y) at x = 3 scaled vertically to have an area equal to one.

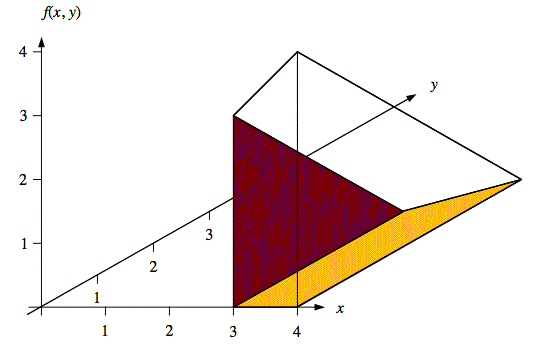
Mathematically, we are using the values of f(x = 3, y).

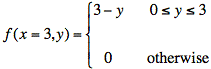
The vertical scaling is taken care of by the integral in the denominator of the equation for conditional probability.

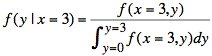
or

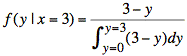
The integral in the denominator is the area of the triangular cross-section at x = 3. We may compute it as one-half base times height or by integrating:

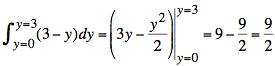
Substituting this value into our earlier equation for f(y | x = 3) gives our answer: