Ex:           Three children, Ann, Bob, and Cal, are running a race. Find all the possible outcomes of the race.

                  A ≡ The sum of the numbers on the dice equals seven.

Sol'n:      A tree diagram helps to solve this problem. We start with a root node to which we attach branches to nodes for all possible first-place finishers. From those nodes we attach branches to nodes for all second-place finishers. Note that the first-place finisher is no longer in the pool of possible second-place finishers. From those nodes we attach branches to nodes for all third-place finishers. Note that only one runner is left for third place.

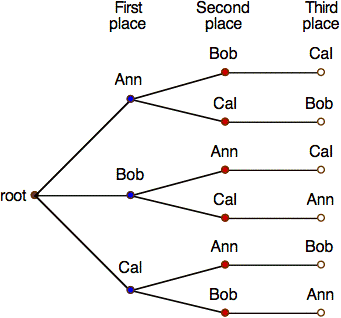
Each complete branch from the root out to a leaf is one possible outcome. Thus, the number of outcomes equals the number of leaves = 6.

Since no runner can finish in more than one place, this is sampling without replacement. Since the order of finish does matter, this is a permutations problem. An alternative to drawing the tree diagram is to use a permutation coefficient:

3P3 ≡ # ways of ordering 3 things taken 3 at a time = 3! = 3⋅2⋅1 = 6