|
|
By: Neil E. Cotter
|
Probability
|
|
|
|
Counting |
|
|
|
Trees |
|
|
|
Ex2 |
|
|
|
|
Ex: Consider flipping a fair coin until two Heads or three Tails are obtained. Find the set of possible outcomes and their probabilities.
Sol'n: A tree diagram shows the possible sequences of flips. The longest sequence we can have is four flips. Some sequences actually end before all four flips are performed, but it is useful to continue the tree to four flips in order to calculate the probability of each sequence. That is, the probability of a sequence is found by summing up the probabilities of all paths from where a sequence ends to the fourth flip. At the fourth flip, all sequences are equally likely. Since there are 24 = 16 possible sequences, the probability of each sequence of length four is 1/16.
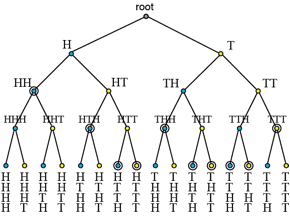
Larger circles at nodes indicate stopping points of sequences. By counting the number of terminal points (leaves) that emanate from each stopping point and multiplying by 16, we get the probability of each sequence.
So P(HH) = 1/4, P(HTH) = 1/8, P(HTTH) = 1/16, P(HTTT) = 1/16,
P(THH) = 1/8, P(THTH) = 1/16, P(THTT) = 1/16, P(TTHH) = 1/16,
P(TTHT) = 1/16, and P(TTT) = 1/8.