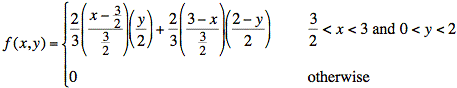Ex:          

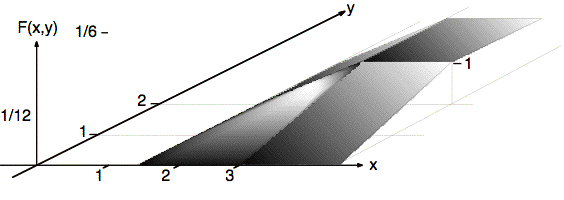
Plot the joint probability density function, f(x, y), for the joint cumulative distribution function, F(x, y), shown above in a cutaway view. Assume that X and Y are independent. The following information is also given:

       

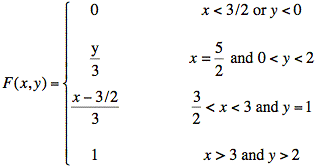
Sol'n:      F(x, y) equals the volume of f(x, y) to the left of x and in front of, (i.e., less than), y. Since F(x, y) = 1 for x > 3 and y > 2, all of the volume of f(x, y) lies in the area where x ≤ 3 and y ≤ 2. Similarly, since F(x, y) = 0 for x < 3/2 or y < 0, all of the volume of f(x, y) lies in the area where x ≥ 3/2 and y ≥ 0.

From the linear growth of F(x, y) in the x direction in the area where f(x, y) is nonzero and on the ramp for 3/2 ≤ x ≤ 3 for y > 2, it follows that the area of the cross section of F(x, y) in the y direction is constant as x changes. Similarly, from the linear growth of F(x, y) in the y direction in the area where f(x, y) is nonzero and on the ramp for 0 ≤ y ≤ 2 for x > 3, it follows that the area of the cross section of F(x, y) in the x direction is constant as y changes.

The simplest solution for F(x, y) is a box of constant height over the region where ƒ(x, y) is nonzero. To achieve a volume of one, the height of the box should be 1/3:

If we integrate this ƒ(x, y), we get a complete description of F(x, y):

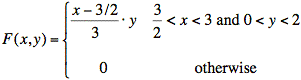
Curiously, another surface also works. This surface has cross sections that have linear slopes on top in both the x and y directions.