Ex:            Consider the rolling of 3 six-sided fair dice. For (a)-(d), determine whether the events are independent. In other words, determine whether the probability of the event to the left of the vertical line is independent of the event to the right of the vertical line. (If they are independent, the conditional probability is the same as the probability of the event to the left of the vertical line.) Use the following notation:

die 1 ≡ number showing on first die

sum 2 ≡ sum of numbers showing on first two dice

sum 3 ≡ sum of numbers showing on all three dice

a)     

b)     

c)     

d)     

Sol'n:  a)  We calculate the conditional probabilities from a chart (not shown) of the 36 equally-likely outcomes for the pair of numbers showing on the first two dice:

or

or

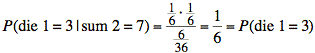
Since the conditional probability is the same as the unconditional probability, the events are independent.

             b) We proceed to calculate the conditional probability as in part (a).

or

or

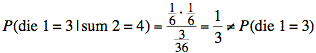
Since the conditional probability is not the same as the unconditional probability, the events are dependent.

             c)  We proceed to calculate the conditional probability as before but using a chart of 216 equally likely outcomes for the three numbers showing on the dice.

or

or

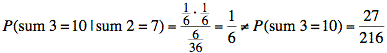
Since the conditional probability is not the same as the unconditional probability, the events are dependent.

             d) Since we found these two events were dependent in part (c), we know they will prove to be dependent again. Nevertheless, we proceed with the calculation as an illustration of this idea.

or

or

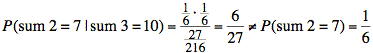
Since the conditional probability is not the same as the unconditional probability, the events are dependent.