Ex:           A joint probability density function is defined as follows:

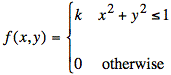
a)      Sketch the shape of f(x, y). (You may assume k = 1 for this sketch.)

b)      Calculate the value of k.

Sol'n: a)  The region, x2 + y2 ≤ 1, on which f(x, y) ≠ 0 is called the support of f(x, y). It is a circle of radius one, centered on the origin, as shown below.

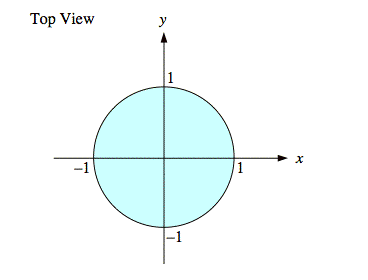
Since f(x, y) = k is constant on its support, f(x, y) is a cylinder as shown below.

             b) The volume of f(x, y) equals one. Since the volume is equal to the area of the support times height k, we have volume = k πr2 where r = 1. It follows that k = 1/π. The illustration, below, shows the 3-dimensional shape of f(x, y) with a height of k = 1/π.