Ex:           Find the probability density function of the average value of 12 independent standard gaussian random variables.

Sol'n:      We want to find the probability density function for Y:

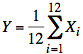
where

Xi ~ n(0,1) are independent standard gaussian random variables

We rewrite the expression for Y to emphasize that it is a linear combination of independent random variables.

Thus, we have the following mean and variance:

Also, the probability density function (pdf) for a linear combination of independent gaussian random variables is a gaussian random variable. Thus, the pdf for Y is the following gaussian distribution:

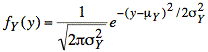
Note:      The pdf for a linear combination of independent gaussian random variables, Xi, is gaussian even when the Xi have differing means and variances.