Ex:           An engineer claims that summing 12 random variables that are independent and uniformly distributed on [0,1] gives a good approximation to the standard gaussian (or normal) distribution. Calculate the mean and variance of 12 independent uniform random variables on [0,1], and determine whether the engineer's claim is valid for the mean and variance. In other words, do you get the mean and variance of the standard gaussian distribution?

Sol'n:      Let X1, ..., X12 be the the 12 random variables that are uniformly distributed on (0,1). Let Z be the random variable we obtain by summing the Xi. We use the following tools for linear combinations of independent random variables (extended from formulas for the sum of two random variables and using a multiplying factor of one for each term):

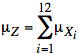
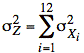
For uniform (0,1) random variables, we have the following values:

                     and                       

Thus, we have the following mean and variance of Z:

           and                       

For a standard gaussian, we have μ = 0 and σ2 = 1. Thus, the engineer has the wrong mean value for Z.

Note:      By subtracting 6 we obtain a fairly good approximation to a standard gaussian. It has the correct mean and variance, and the shape is nearly gaussian. The flaw it still has is that the tails extend only to −6 on the left and +6 on the right. It is an acceptable substitute for the gaussian, however, if having values far out on the tails are unimportant.