Tool:       Given probability density function, fX(x), for X, the probability density function (pdf),

fY(y) for Y = aX + b, (a ≠ 0),

is

.

Also, the mean and variance transform as follows:

.

Proof:     By definition, fY(y) is the derivative of the cumulative probability distribution function.

Making a direct substitution for Y, we have an expression that we can transform into a statement about the probability of X:

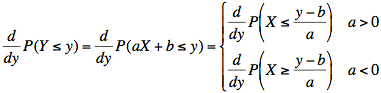
The last expressions are statements about the cumulative distribution function of X.

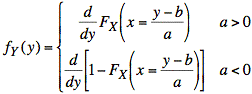
Using the chain rule from calculus, it is possible to write the above derivatives in terms of x:

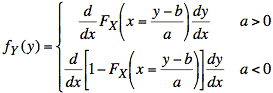
The derivatives in terms of x are probability density functions for X, and the derivatives of y = ax + b are equal to a:

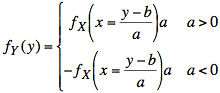
This may be written more compactly as follows:

For the mean of Y, we write the integral formula:

We rewrite the integral in two parts and exploit the property that the area under the pdf is equal to one:

For the variance, we substitute for Y in the variance formula:

or