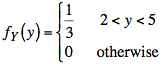Ex:            If X is uniformly distributed on the interval [0, 1], i.e., X~u[0, 1], find the probability density function (pdf) for Y = 3X + 2.

Sol'n:       For Y = aX + b, (a ≠ 0), the pdf for Y in terms of the pdf for X is given by the following formula:

For X, we have a uniform pdf on [0, 1]:

Using a = 3 and b = 2 in the formula for fY(y), we make a literal substitution of in the expression for fX(x) and multiply by :

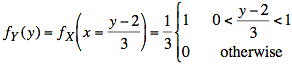
Rewriting the inequality, we have the following form: