Ex:            If X has a gaussian (i.e., normal) distribution with mean μX = 1 and standard deviation σX = 2, i.e., X~n(1, 2), find the probability density function for Y = −X + 9.

Sol'n:       For Y = aX + b, (a ≠ 0), the pdf for Y in terms of the pdf for X is given by the following formula:

For X, we have a gaussian or normal pdf:

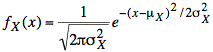
Using the formula for fY(y), we have one form for fY(y):

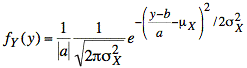
Using a = −1 and b = 9 in the formula for fY(y), we have one form of the final answer:

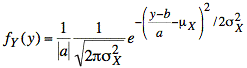
This is again a gaussian or normal distribution and, after some algebraic manipulation, we find that the gaussian or normal distribution has the following mean and variance:

Using a = −1 and b = 9, we have another form for the desired answer: