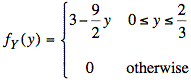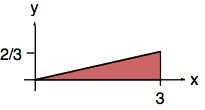
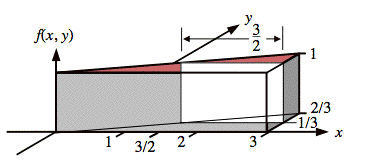
Ex:           Given joint probability density function f(x, y) = 1 on the area of the x,y-plane shown below, find the marginal probability density functions, f_X(x) and f_Y(y).

Sol'n:      The illustration below shows a 3-dimensional view of f(x, y).

The value of f_X(x) at a given value of x is the area of the cross section of f(x, y) in the y direction. In the illustration below, the value of f_X(x = 3/2) is shown to be equal to 1/3 ⋅ 1 (i.e., width ⋅ height) = 1/3.

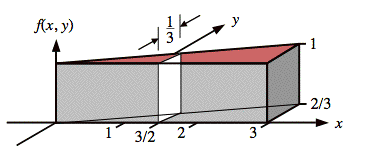
Since the cross-sectional area has a width that grows linearly as x increases from 0 to 3, we can write down a formula for f_X(x) directly:

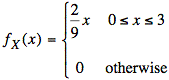
Mathematically, we get the same answer by integrating f(x, y) in the y direction. We must, however, correctly determine the limits of integration. We do so by considering a top view of the support (or footprint) of f(x, y) on the xy-plane:

For a given value of x between 0 and 3, y has values between y = 0 and y = . Thus, the upper limit of the integral for f_X(x) depends on x:

Completing the calculation, we get our answer, (which is the same as before):

Similar arguments apply for the calculation of f_Y(y). The graphical approach relies on calculation of areas of cross sections in the x direction. In contrast to cross sections in the y direction, the area of the cross sections in the x direction decrease in area as y increases. The diagram below shows that the cross section for y = 1/3 has area equal to 3/2 ⋅ 1 (i.e., width ⋅ height) = 3/2.

Since the cross-sectional area has a width that decreases linearly as y increases from 0 to 2/3, we can write down a formula for fY(y) directly:

Mathematically, we get the same answer by integrating f(x, y) in the x direction. As before, we must correctly determine the limits of integration. From the top view of the support (or footprint) of f(x, y) on the xy-plane we see that, for a given value of y between 0 and 2/3, x has values between x =  and x = 3.

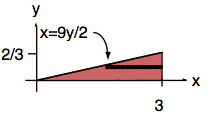
This time, the lower limit of the integral for f_Y(y) depends on y:

Completing the calculation, we get our answer, (which is the same as before):