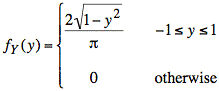Ex:           A joint probability density function is defined as follows:

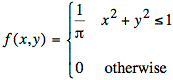
Find the marginal probability density functions, f_X(x) and f_Y(y).

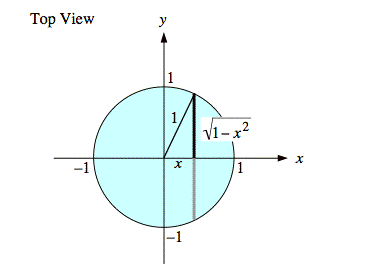
Sol'n:      The region, x2 + y2 ≤ 1, on which f(x, y) ≠ 0 is called the support of f(x, y). It is a circle of radius one, centered on the origin, as shown below. The diagram also shows the calculation of the vertical segment over which f(x, y) ≠ 0 as a function of position x.

The illustration, below, shows the 3-dimensional shape of f(x, y) with a height of k = 1/π. The figure also shows a cross section in the y direction at one value of x.

The value of f_X(x) at one value of x is equal to the area of the cross-section of f(x, y) in the y direction at that value of x. We use the diagram of the support (or footprint) of f(x, y) to determine the limits of integration in the following calculation that determines the area of the cross-section.

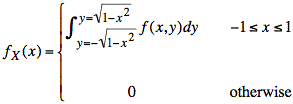
Note that the restriction on x is the entire width of the figure, since the cross-sections in the y direction are nonzero over this width.

f(x, y) = 1/π over the interval of integration. Thus, the value of the integral is just the length of the interval of integration times 1/π:

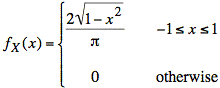
By symmetry, we obtain a similar result for fY(y):