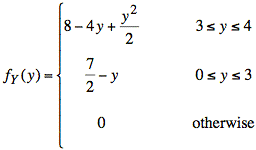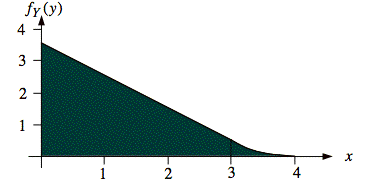
Ex:           A joint probability density function is defined as follows:

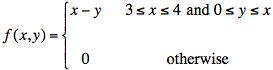
Find the marginal probability density function, f_Y(y). Note that the condition 0 ≤ y ≤ x depends on x.

Sol'n:      The region, 3 ≤ y ≤ 4 and 0 ≤ y ≤ x, on which f(x, y) ≠ 0 is the support of f(x, y). It is a trapezoid, as shown below. The diagram also shows several horizontal segments over which f(x, y) ≠ 0 as a function of position y.

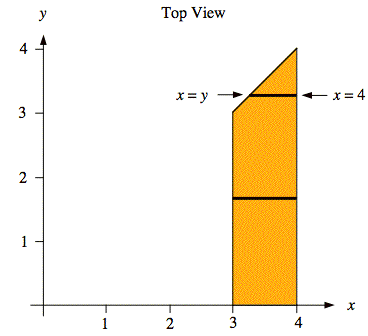
The illustration, below, shows the 3-dimensional shape of f(x, y). The figure also shows cross-sections in the x direction. The value of f_Y(y) at any value of y is equal to the area of the cross-section of f(x, y) in the x direction at that value of y.

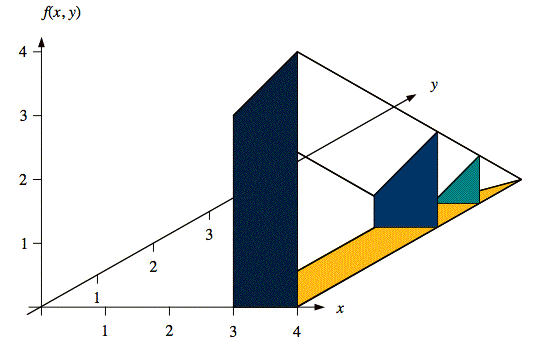
We use the diagram of the support (or footprint) of f(x, y) to determine the limits of integration in the following calculation that determines the area of the cross-section.

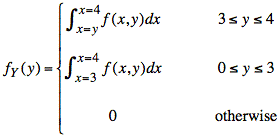
Substituting f(x, y) = x − y into the integral, we evaluate f_Y(y).

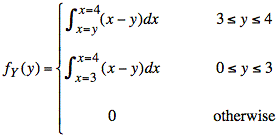
or

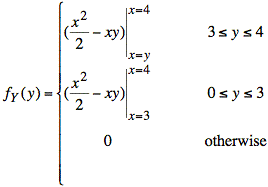
or

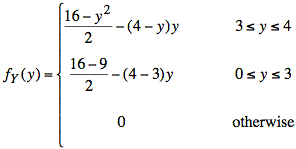
or