Ex:           Prove the following:

a)     E(X) = center of mass of the density function, f(x). That is, show

       

b)     E(X) may be computed from centers of mass of pieces concentrated at single points. In other words, show that, for segments that cover x = (−∞,∞) without overlapping, we may reduce the "mass" of f(x) to single points:

        defines mass for ith segment of f(x)

        defines center of mass for ith segment of f(x)

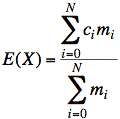        , or 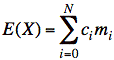since total probability (mass) = 1.

Pf:      a)   We break the integral into pieces and observe that E(X) is a constant that we may take outside the integral:

Since the total probability is equal to unity, the last integral has a value of unity and we obtain a value of zero, as desired:

            b)   Given , we have
.

Thus, 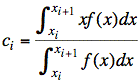. We substitute this and the definition for mi into the center of mass formula:

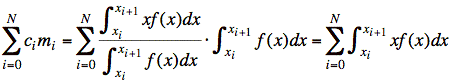
The expression on the right is just the integral from −∞ to ∞ broken into N pieces that are then put back together by the summation. Thus, we have

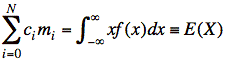, and the proof is complete.