Ex:           Given X~u(0, 1), (i.e., X is uniformly distributed from 0 to 1), find the probability density function, fY(y), for Y where

.

Sol'n:      The transformation from X to Y is a strictly increasing function, g(X):

Thus, we may use an identity for nonlinear transformation of random variables:

The inverse function, g−1(y), is found by solving for X in terms of Y:

Making the substitution for g−1(y), we have the following expression for fY(y):

To simplify the first term on the right side, we start with the definition of the probability density of X:

Wherever x appears in the definition of fX(x), we substitute g−1(y):

or

Now we rewrite the inequality involving −ln(1 − y) in terms of y:

or

or

Note:      If fX(x) is more complicated than the simple uniform density function considered here and has values that are functions of x, then we would also replace those values of x with g−1(y), too.

Consider the following example with the same g(x) as in the present problem:

We would substitute x = g−1(y) for every x:

or

Returning to the problem at hand, we now consider the second term of the expression for fY(y):

Taking the derivative yields the expression for the second term:

This term will multiply the first term:

or

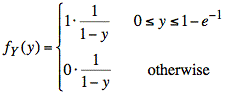
or

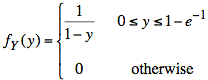
Note that, although g( ) involved an exponential and g−1( ) involved a log function, the expression for fY(y) contains neither of these.