Ex:           An engineer is analyzing a diode circuit in which there is a very small voltage across the diode. The current in the diode is given by the following equation:

The voltage is small enough that a quadratic approximation (obtained from a Taylor series expansion) for the exponential is sufficiently accurate:

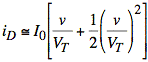
In the next stage of the circuit, the first order term is removed by a current summation, (or subtraction), but a quadratic noise current remains:

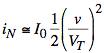
With these preliminaries given, your task is to use the last equation and find the probability density function for iN, assuming X ≡ v/VT has a random value uniformly distributed between 1 and 2, (i.e., X~u[1,2]). To make matters simpler, you need only show that the probability density function for iN = X2⋅I0/2 is given by the following expression:

Hint: Define Y ≡ iN ≡ I0/2⋅X2. Then take the derivative (d/dy) of the cumulative distribution function for y, F(y), defined in terms of X. In other words, fill in the ?'s and f(x)) in the following equation:

Sol'n:      First, we observe that the value of cumulative distribution at x, (i.e., FX(x)), for a uniform distribution on (1, 2) is the area to the left of x and will grow linearly from 0 to 1 as x goes from 1 to 2.

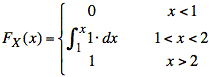
Thus, we have the following expression for FX(x):

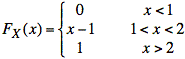
Substituting for x, we have the expression for FY(y):

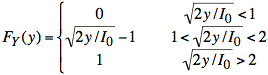
We translate the inequalities into expressions for y:

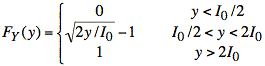
Taking the derivative gives fY(y):

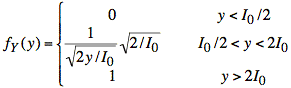
or

This is the result given in the problem statement when we substitute iN for y.