Ex:           In communications theory, a transmitted bit value with additive noise is often modeled as a one or zero plus a gaussian distributed random variable. In a certain quadrature modulation scheme, transmitted pairs of bits may be treated as points at (−1, −1), (−1, 1), (1, −1), and (1, 1) plus an ordered pair of random variables, X and Y, drawn from a two-dimensional gaussian distribution with correlation ρXY and zero means:

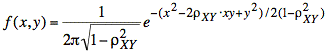
where

To determine which pair of bits is sent, one computes f(x, y) for each of the points at (−1, −1), (−1, 1), (1, −1), and (1, 1). The point with the largest value of f(x, y) is taken as the bit pair that was originally sent. It turns out that the point with the largest value of f(x, y) is the point closest to (X, Y).

Normally, X and Y are unknown, but suppose that a measurement of Y is available, and suppose that Y = 1/3. If a (−1, −1) is transmitted, find the probability that (−1 + X, −1 + Y) is closer to (1, −1) than to (−1, −1).

Sol'n:      We consider a diagram showing the signals and noise.

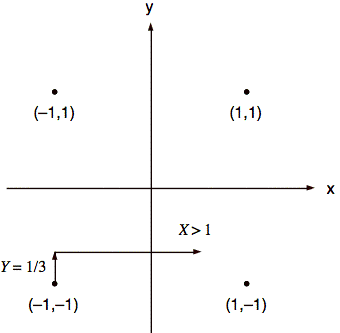
For the received signal to be closer to (1, −1) than to (−1, −1), the value of X must be greater than 1, as the diagram shows. Thus, we find the conditional probability f(x | y = 1/3) and determine the conditional probability that X > 1.

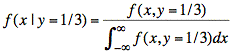
We compute the integral in the denominator by factoring out the integral of a gaussian distribution whose value must be equal to one. Our first step in this process is to substitute numerical values for ρ and y.

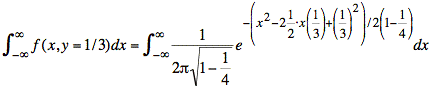
or

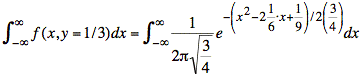
Now we complete the square in the exponent so we will have something that is of the form (x − μX)2. We add and subtract terms of the same value. The extra constants that are not part of the square in the exponent may be extracted as multiplicative factors, since exponents add.

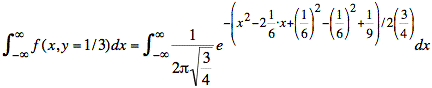
or

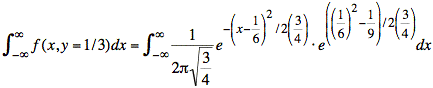
We now take the constant exponential terms outside of the integral, and we also extract a factor of the square root of 2π, leaving the integral of a gaussian distribution whose mean is 1/6 and whose variance is 3/4:

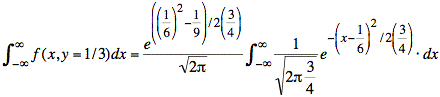
or

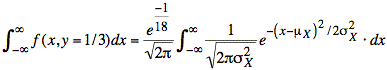
where

μX = 1/6 and

The value of the integral of the gaussian is one, and we have the final value we are seeking:

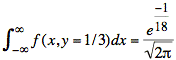
Now we evaluate the conditional probability we originally set out to find:

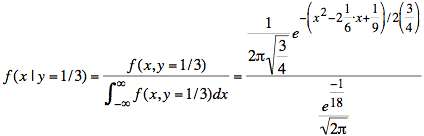
If we complete the square in the exponent, as before, we get

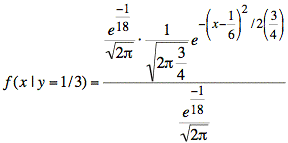
or

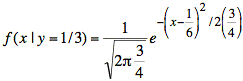
Note:      The mean is m = ry and the variance is s2 = 1 − r2. This will always be the case, and we may dispense with the lengthy calculation.

Now we find P(X > 1). This is equal to 1 − F(x = 1) where F(x) is the cumulative distribution for f(x | y = 1/3). We use the formula that converts the value of x to the value of z for a standard gaussian random variable:

Using the mean and variance of our conditional probability and X = 1, we have the following:

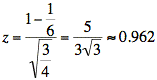
From a table of values for the cumulative distribution, F(z), of a standard gaussian, we obtain the value F(0.962) = 0.832. Thus, our final answer is as follows: