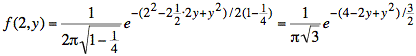Ex:            The probability density function for a 2-dimensional gaussian (or normal) distribution is described by the following formula:

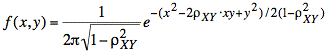
where ρXY = 1/2

a)      Make a (1-dimensional) plot of a cross-section of f(x, y) on the line x = 2 (while y varies from −∞ to ∞). Describe the shape of this curve. Determine whether this curve is a valid probability density function.

b)      Make a (1-dimensional) plot of a cross-section of f(x, y) on the line y = 2x. Describe the shape of this curve. Determine whether this curve is a valid probability density function.

Sol'n:  a)  The function we are plotting is f(2, y):

The plot of f(2, y) shown below was generated with Matlab® code:

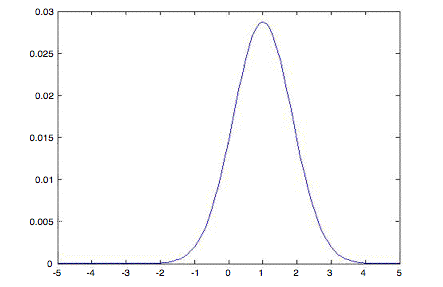
The shape of f(2,y) is similar to a gaussian distribution. For it to be a valid pdf, it must have a total area equal to one. We cannot integrate f(2,y) directly, but we can use the method of completing the square to write the exponent as y minus a constant—corresponding to the mean value of y—squared over a constant—corresponding to the variance.

To achieve the desired form, we extract a factor of e−2 from the exponential. Now we can write f(2,y) in the form of a gaussian multiplied by a constant.

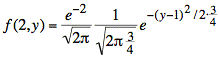
The constant multiplying the gaussian in this case is . Thus, the area under f(2,y) is rather than 1. Thus, this slice of the 2-dimensional gaussian is not a gaussian.

             b) The plot in this second case requires a bit more work. To achieve the correct scale, the distance from the original must be faithfully preserved. Using a parameterized curve, we achieve the desired result. Let t be the distance from the origin along the line y = 2x. If t = 1, then the Pythagorean theorem dictates that and . In general, we have and . Using these values, we obtain the plot shown below, generated in Matlab®.

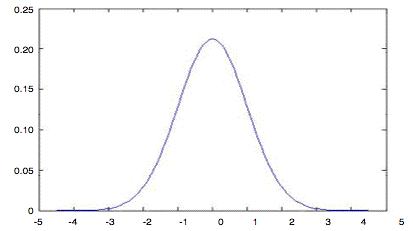
As before, we can write in terms of a gaussian distribution.

or

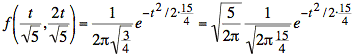
We have a gaussian distribution multiplied by . Thus, the area under the curve is rather than 1, and the curve is not a valid pdf.