CONCEPTUAL TOOLS

By:  Neil E. Cotter

Probability

 

 

Prob density func, f(x)

 

 

Chi-squared distribution

 

 

χ2 derivation
 
 
 

 

Deriv:      The following is a simplified derivation showing that the probability density function (pdf) for the normalized sample variance, , is the χ2-distribution with n = n – 1 degrees of freedom where n is the number of independent, normally distributed samples, s2 is the variance of each sample, and sample variance s2 is defined in the standard way:

                                                                                     (1)

where the Xi are the samples, and  is the sample mean defined in the standard way:

.                                                                                                      (2)

To improve clarity and focus attention on key ideas in the derivation, we assume the samples are drawn from a standard normal distribution with mean μ = 0 and variance σ2 = 1:

.                                                                                        (3)

Based on rules for linear combinations of random variables, the sample mean is normally distributed with variance s2/n = 1/n since we are assuming s2 = 1.

                                                        (4)

The pdf for all the samples is an n-dimensional normal distribution [1].

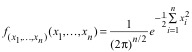                                                            (5)

With some manipulation of summations [2], we may show that the summation of the squared xi's may be written in terms of the sample variance and sample mean:

.                                                                                   (6)

or

.                                                                                (7)

Using (6), we rewrite the n-dimensional normal distribution:

.                                              (8)

We find the pdf of x = (n – 1)s2 by taking the derivative of the cumulative distribution function.

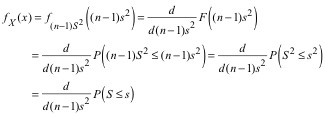                (9)

Given (8) and (9), our goal will be to express P(S ≤ s) in terms of s, but our starting point is to find the cumulative probability by integrating the pdf of (x1, ..., xn) over all the (x1, ..., xn) that would give a sample variance that is less than or equal to s2.

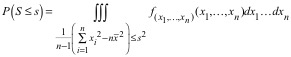                         (10)

or

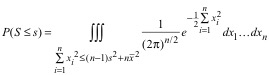                                 (11)

We observe that the pdf  is spherically symmetric, which suggests that we might be able to use spherical coordinates for our integral.  However, the spherical symmetry of  is with respect to the origin, whereas we want to integrate over the (x1, ..., xn) that are within a certain squared distance from .  That is, (n – 1)s2 may be thought of as a measure of the squared distance from (x1, ..., xn) to (, ..., ):

.                                                                                 (12)

It follows that the (x1, ..., xn) are points in an n‑dimensional sphere centered at  at a squared distance of at most (n – 1)s2 or a radius of .

 

For a given , however, these (x1, ..., xn) must also lie on the hyper-plane of points such that  since the average of the xi is .  This plane is perpendicular to  or a vector in the (1,1,1) direction.  Thus, for a given , we are integrating over the intersection of an n-dimensional sphere of radius  and a hyper-plane in n dimensions that is perpendicular to the (1,1,1) direction.  The resulting intersection is an (n–1)-dimensional sphere.  As shown in Fig. 1(a), for the case of n = 2, (2-dimensional space for X1, X2), the (n–1)-sphere is a 1-dimensional line of points on the constant  line, and as shown in Fig. 1(b), for the case of n = 3, (3‑dimensional space for X1, X2, X3), the (n–1)-sphere is a
2-dimensional circle of points on the constant  plane.

 

We may use  and r as orthogonal variables of integration.  As we vary , the line of constant  moves a distance  in the (1,1) direction, and sphere of integrated points moves with it.  This gives an extruded (n–1)-dimensional sphere as the region of integration.  As shown in Fig. 2(a) for the case of n = 2, the region of integration is an infinite band in the (1,1) direction, and as shown in Fig. 2(b) for the case of n = 3, the region of integration is an infinite cylinder in the (1,1,1) direction.

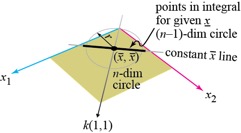
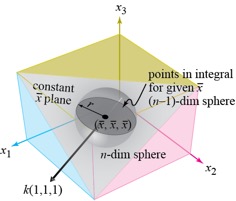
      (a)                                                                             (b)

Fig. 1.  Points to integrate in the r direction for calculation of P(S ≤ s) at a given value of :
(a) 2-dimensional case, (b) 3-dimensional case.

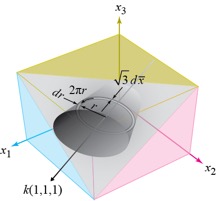
               (a)                                                                    (b)

Fig. 2.  Region of integration for calculation of P(S ≤ s) in coordinates of  and r:
(a) 2‑dimensional case is infinite band parallel to (1,1) direction,
(b) 3-dimensional case is infinite cylinder parallel to (1,1,1) direction.

For n ≥ 2 dimensions, the above picture generalizes to the following change of variables:

.                                                                        (13)

where  varies from –∞ to ∞ and An–1(r) is the surface area of an (n–1)-dimensional sphere of radius .

From [3] we have the following formulas for sphere volumes and surface areas:

 is the volume of an n-dimensional sphere of radius r               (14)

 is the surface area of an n-dimensional sphere of radius = 1. (15)

It follows that the surface area of an n-dimensional unit sphere is:

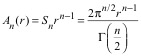.                                                                          (16)

The gamma function has the following properties [4]:

 for n > 0 a positive integer

 for all complex z except integers ≤ 0

 

Using (16), we have:

.                                                              (17)

We now have the following integral for P(S ≤ s):

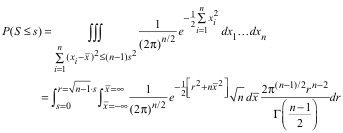.       (18)

We separate variables, and perform the inner integration first (after ensuring that the inner integration is of a normal density function, thus yielding a value of unity).

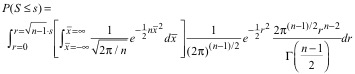    (19)

The value inside the square brackets is our integral (of a normal density function) that has a value of unity.  Thus, we have

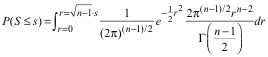.                                (20)

We now use ν = n – 1 as the "degrees of freedom" to simplify the expression and reflect the idea that the pdf is analogous to one for n – 1 variables.

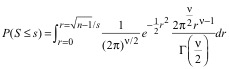                                              (21)

Fortunately, we will take the derivative of the cumulative distribution, so computing the integral is unnecessary.  However, we do have to deal with a change of variables for the derivative.

As a preliminary to using the chain rule, we have the following calculations:

                                                                                              (22)

so

                                                                                                              (23)

and

.                                                                                                        (24)

Using the chain rule, we have the following result:

.                                         (25)

The final derivative is the derivative of an integral, so the final derivative is just the integrand from (21):

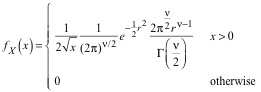                                   (26)

or, since r2 = x and several constants cancel out,

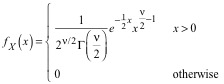.                                               (27)

 

In conclusion, the distribution of x = (n – 1)s2 when s2 = 1 is a chi-squared distribution.  Without proof, we state the following result when s2 ≠ 1:

The probability density function of  is a chi-squared distribution with n = n – 1 degrees of freedom [2]:

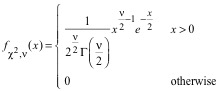                                                (28)

 

Ref:    [1] "The Multivariate Normal Distribution." http://www.math.uah.edu/stat/special/MultiNormal.html

            [2] Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye, Probability and Statistics for Engineers and Scientists, 8th Ed., Upper Saddle River, NJ: Prentice Hall, 2007.

      [3] Weisstein, Eric W. "Hypersphere." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Hypersphere.html

      [4] Weisstein, Eric W. "Gamma Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/GammaFunction.html