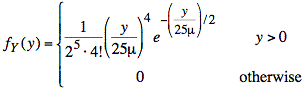Ex:           An engineer wishes to estimate the average "power" for a noise signal observed on an oscilloscope. The engineer averages the squares of 10 samples of the signal to calculate a value called Y:

If the Xi are independent gaussian distributed random variables with mean equal zero and variance equal (5 mV)2, (which is the true so-called "power"), find an expression for the probability density function of Y.

Note that this probability density function tells about the variability of the engineer's estimate of the power when only 10 values are used.

Sol'n:      A sum of 10 independent standard gaussian random variables has a chi-squared distribution with 10 degrees of freedom. The Xi in this problem have a mean of zero, but their variance is 5 mV and we are multiplying each term by 1/10 to take the average. Thus, we have something slightly different than a sum of standard gaussian random variables.

One way to deal with this problem of nonstandard gaussians is to observe that our Xi are equivalent to standard gaussians, Zi, multiplied by 5 mV. Thus, we may factor out a sum, W, of the squared Zi's.

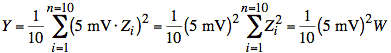
where

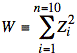
For W, we have a chi-squared distribution with 10 degrees of freedom:

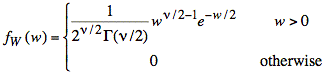
Since Y is just a scaled version of W, we may apply the following identity for Y = aW:

Thus, we obtain the symbolic probability density function for Y:

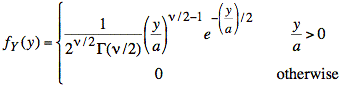
Plugging in numerical values of ν = 10 for the degrees of freedom and a = (5 mV)2/10 = 2.5 μV2 for the scaling factor, and using the identity for the gamma function, Γ(n) = (n − 1)! = 4! for integer n = ν/2 =5, we obtain the numerical probability density function for Y: