Ex:            In a communication system, single bits are communicated by short snippets of waveforms of different shapes for 0's and 1's. At the receiving end, the waveform for one bit is sampled 8 times. Noise in the form of gaussian (or normally) distributed values is effectively added to each sample. The noise samples, Xi, are independent and identically distributed with mean value and variance :

Whether a 0 or 1 is received correctly depends on the total power in the eight noise samples for each bit. This noise power, W, is calculated as the sum of the squares of the values of the eight Xi's.

Find the probability density function (pdf), fW(w), of W.

Sol'n:       The sum, X, of squares of ν random variables, Xi, with identical, independent, standard gaussian (or standard normal) distributions yields a chi-squared distribution of degree ν, [1]:

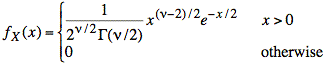
with mean value μ = ν and variance σ2 = 2ν.

In this problem, the Xi are independent gaussian random variables but with variances equal to 2.25 instead of 1. Thus, the challenge is to rewrite the sum of squares of the Xi in terms of a sum of squares of standard gaussian (or standard normal) random variables, Yi.

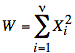
Since the Xi have zero mean, they may be written as scaled standard gaussians. In other words, they are linearly transformed standard gaussians:

where a =  = 1.5.

Note:       A linearly transformed gaussian is a gaussian. If X = aY + b, for example, we have the following probability density for X:

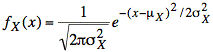
where

and

If we express W in terms of Yi's, we find that it is a linear transform of a chi-squared random variable:

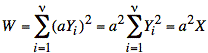
where X is chi-squared of degree ν.

Now we can apply the tool for the pdf of a linear transform of a random variable:

If W = aX + b, (a ≠ 0), then .

Also, the mean and variance transform as follows:

Using this tool, our pdf for W is the following:

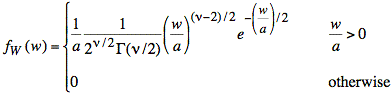
where a = 1.5.

Ref:    [1] Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye, Probability and Statistics for Engineers and Scientists, 8th Ed., Upper Saddle River, NJ: Prentice Hall, 2007.