Ex:           An engineer is analyzing a circuit in which there is a diode. The current in the diode is given by the following equation:

If Y ≡ v/VT is gaussian distributed with mean value μY = 0.7V/26mV and variance , find the probability density function of Z = .

Sol'n:      We observe that, given Y is gaussian distributed, the following random variable, X, has a lognormal distribution:

This is slightly different from the Z we are interested in, but it differs only by a horizontal shift by a value of one:

Thus, we start with the probability density function for Y and then determine how to make the shift to Z.

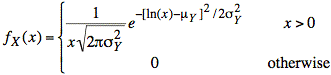
Now we write X in terms of Z:

Making this substitution for X we obtain the following result:

or

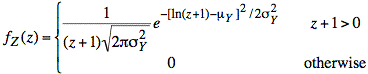
or

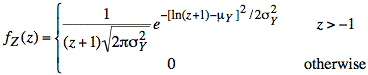
NOTE:     To determine whether we should add or subtract one when substituting for x, we observe that when x = 0 we have z = −1, and we should have the same probability density for x = 0 and z = −1. This implies that a term equal to x in fX(x) should be replaced by a term that adds 1 to z so the value of the term will again be zero.