Ex:            A sample-and-hold circuit is used in an A/D converter to store a voltage on a capacitor while it is being translated into a binary number. As with any capacitor, the stored charge on the capacitor leaks away over time. The loss of voltage is modeled by a capacitor discharge equation:

where

  V ≡  voltage on capacitor when A/D conversion is complete (volts)

v0 ≡  initial voltage on capacitor = 1 V for this problem

    T ≡  time required for A/D conversion = gaussian distributed random variable with
mean 20 ns and variance (2 ns)2

RC ≡  time constant for leakage = 6 μs

a)      Find the probability density function, fV(v), of the voltage on the capacitor at the end of the A/D conversion.

b)      Find the probability that the voltage on the capacitor droops enough for a 1-bit error in an 8-bit value. In other words, find P(V ≤ v0⋅255/256). Hint: translate the problem into that of finding a probability for a gaussian random variable and use Table A.3 in the course text to find that probability.

Sol'n:  a)  Because T is gaussian (or normal) and appears in the exponent, the form of V is almost a lognormal distribution. The form of the lognormal probability density function (pdf), [1], requires that the entire exponent be gaussian:

where Y is gaussian distributed has lognormal pdf, fX(x), as follows

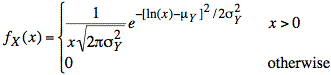
where

         

In the present problem, we have and V replaces X. This is a linear transformation of a gaussian distribution, which is again a gaussian distribution. The mean and variance of this gaussian are as follows:

and

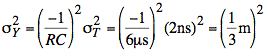
Replacing X with V in the lognormal pdf, we have our final expression for fV(v).

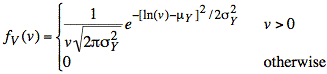
             b) We find P(V ≤ v0⋅255/256) by substituting for V in terms of T and using the cumulative distribution for T:

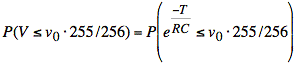
or

or

or

Now we convert T to is equivalent value for a standard gaussian (or normal) distribution:

This means we use the value of t to find the value of z in the cumulative distribution, FZ(z):

Using a table for the cumulative distribution of the standard gaussian, [1], we lookup the value of the probability:

Thus, we have the following final result:

Ref:    [1] Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers, and Keying Ye, Probability and Statistics for Engineers and Scientists, 8th Ed., Upper Saddle River, NJ: Prentice Hall, 2007.