Ex:          

A probability density function is shown above and is described by the following equation:

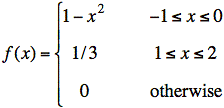
a)     Plot the cumulative distribution function, F(x), for X.

b)     Find P(1/2 ≤ x ≤ 3/2)

c)     Calculate σ2 for X.

Sol'n: a)  F(x) is the integral from −∞ to x of f(x) or, equivalently, the area under f(x) to the left of x:

Because the definition of f(x) changes with x, we break the integral into segments and use only the segments that are left of x:

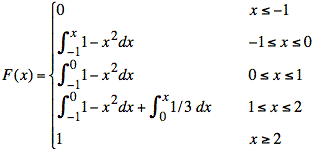
Note that the last entry is 1 because we know the total area under f(x) equals one. Calculating the integrals, we have

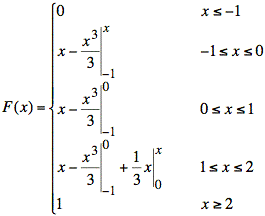
or

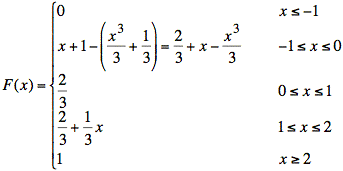
Unless F(x) contains delta functions, the plot of F(x) must be continuous.

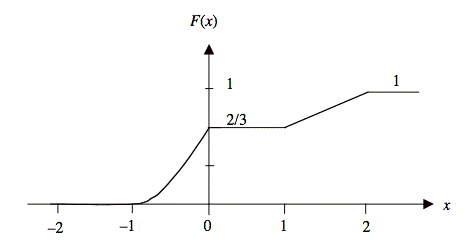
             b) By definition, F(x) = P(X ≤ x). It follows that

P(1/2 ≤ x ≤ 3/2) = F(3/2) − F(1/2)

From part (a), we have F(3/2) = 5/6 and F(1/2) = 2/3. Thus,

P(1/2 ≤ x ≤ 3/2) = 5/6 − 2/3 = 1/6.

Another way to obtain this result is to integrate the probability density function:

P(1/2 ≤ x ≤ 3/2) = 

             c)  The variance, σ2, is given by the formula σ2 = E(X2) − μ2. First, we calculate μ:

or

Second, we calculate E(X2):

or

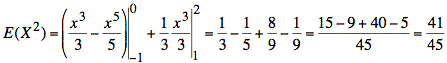
Combining results, we have