CONCEPTUAL TOOLS	By:  Neil E. Cotter	RLC circuits
		General RLC solution
		Summary

---

Tool:        Series and parallel RLC circuits may be solved by a step-by-step procedure outlined below in (a)-(d).  Figs. 1 and 2 illustrate series and parallel RLC circuits.  Note that the circuitry to which the L and C are connected is converted to a Thevenin equivalent, which turns all the R's in the circuit into a single R.

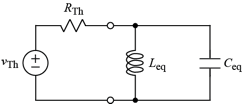
Fig. 1.  Series RLC circuit.                                 Fig. 2.  Parallel RLC circuit.

Series or parallel RLC:

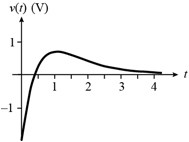
Over-damped:                    s1,2   real, negative, distinct

  also applies to

Critically-damped:             s1 = s2 = –a   real, negative, repeated

  also applies to

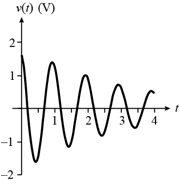
Under-damped:                 s1,2 = –a ± jwd   complex, distinct

   damping frequency

  also applies to

Final value:

:    Use L = wire, C = open.

   also applies to

Initial value:

t = 0–:      Find iL(t = 0–) and vC(t = 0–).

t = 0+:      Find v(t = 0+)   (or whatever variable is being solved for)

                        Use iL(t = 0+) = iL(t = 0–) and vC(t = 0+) = vC(t = 0–).

                        Use L = i-source of value iL(t = 0+), C = v-source of value vC(t = 0+).

                        Find v(t = 0+) from circuit.

                        Equate v(t = 0+) from circuit with v(t = 0+) for symbolic solution.

Initial value of derivative:  

t > 0:        Model L as i-source of value iL and C as v-source of value vC.

Write expression for v(t) (or whatever variable is being solved for) in terms of iL and vC.

t = 0+:      Take derivative of both sides of this expression for v(t) (or whatever variable is being solved for) and evaluate at t = 0+.

                        Use  and/or

                        Complete the calculation of  from circuit.

                        Equate  from circuit with  for symbolic solution.